Solar wind discontinuities spatial evolution and energetic ion scattering

AGU23 poster

Abstract

Because solar wind plasma flow transports the entire spectrum of magnetic field fluctuations (from low-frequency inertial range to electron kinetic range), it is a natural laboratory for plasma turbulence investigation. Among the various wave modes and coherent plasma structures that contribute to this spectrum, one of the most important solar wind elements is ion-scale solar wind discontinuities. These structures, which carry very intense current, have been considered as a free energy source for plasma instabilities that contribute to solar wind heating. Investigations of such discontinuities have been mostly focused on their magnetic field signatures; much less is known about their role in scattering of energetic ions. In this studay, we consider observational-based model of ion dynamics and scattering in force-free rotational magnetic discontinuities. Focusing on quantification of the scattering effect, we demonstrate that background sheared magnetic field plays an important role in determining the efficiency of pitch angle scattering. We provide a model included statistical properties of solar wind discontinuities and providing estimates of ion scattering rate.

Poster PDF

Main findings

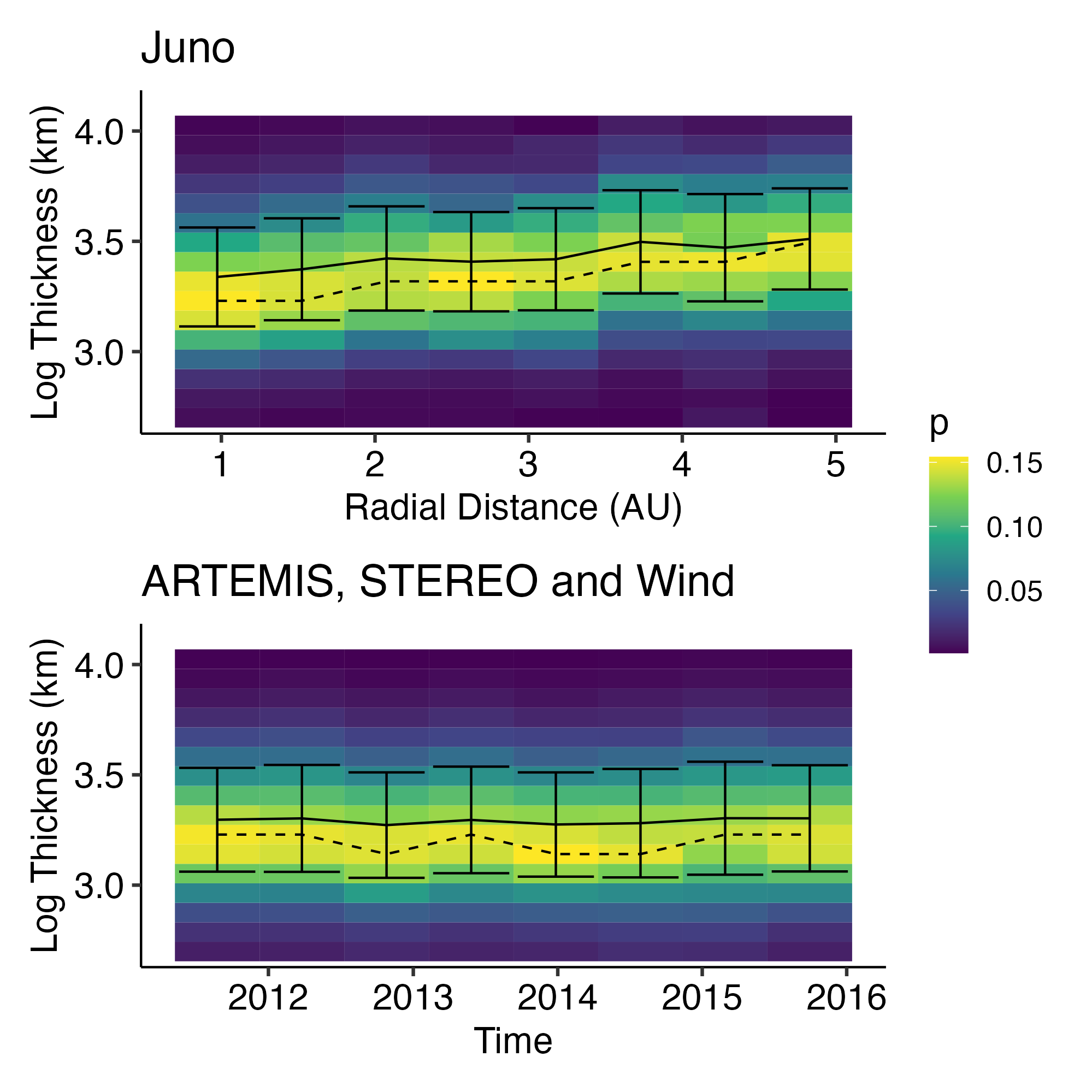
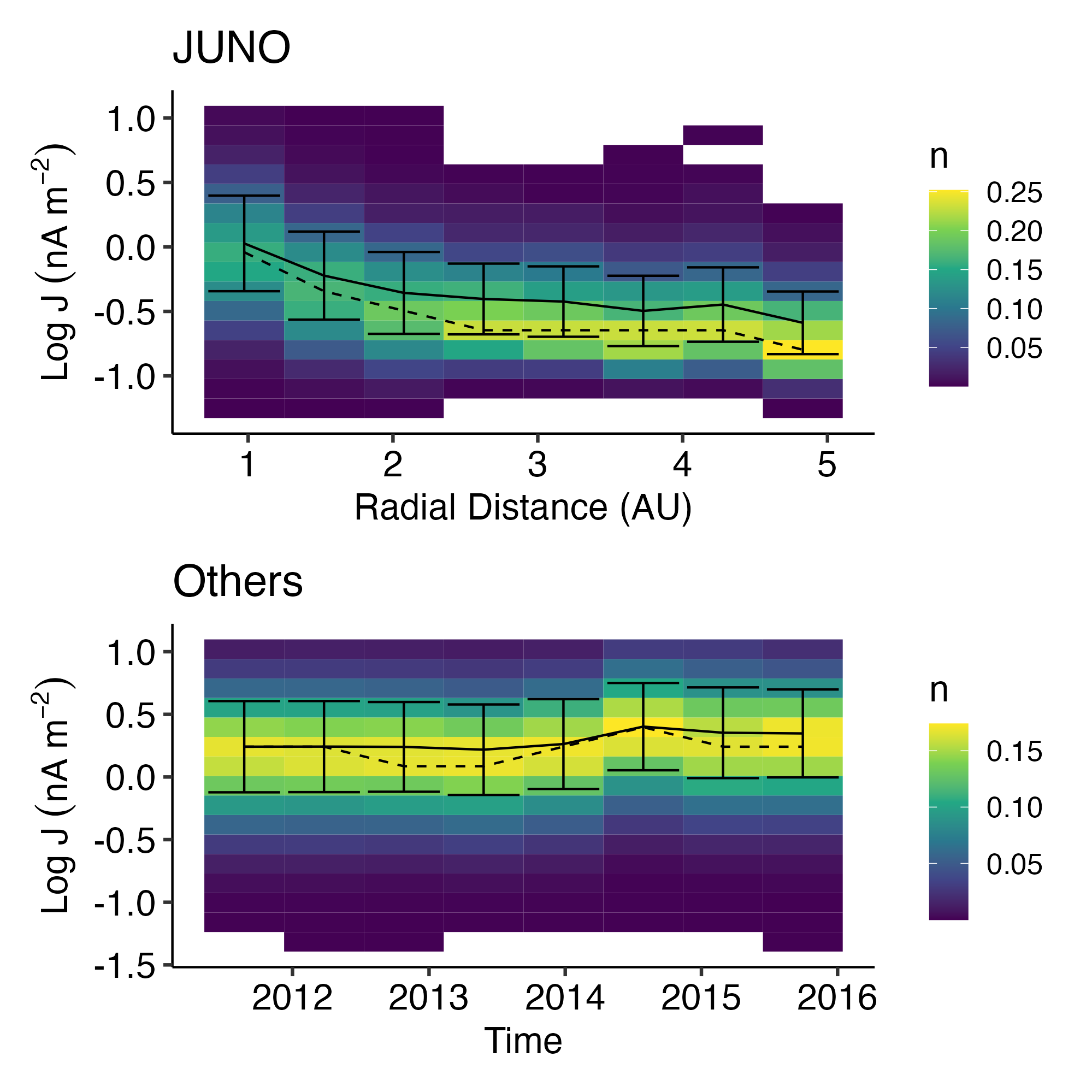
• Solar wind discontinuities evolve in space with occurrence rate decreasing, thickness increasing and current density decreasing with distance from the Sun. And they are probably generated locally beyond 1 AU.
• Background sheared magnetic field plays an important role in determining the efficiency of ion pitch angle scattering, and characterize three ion populations: transient, trapped, regular.

Introduction & Motivation

‘Discontinuities’ are discontinuous spatial changes in plasma parameters/characteristics and magnetic fields (colburn1966?).

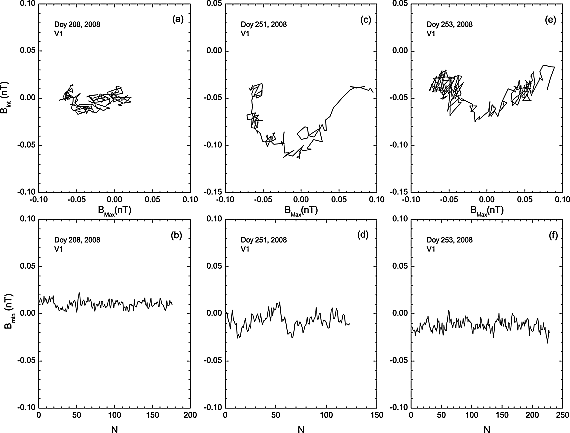
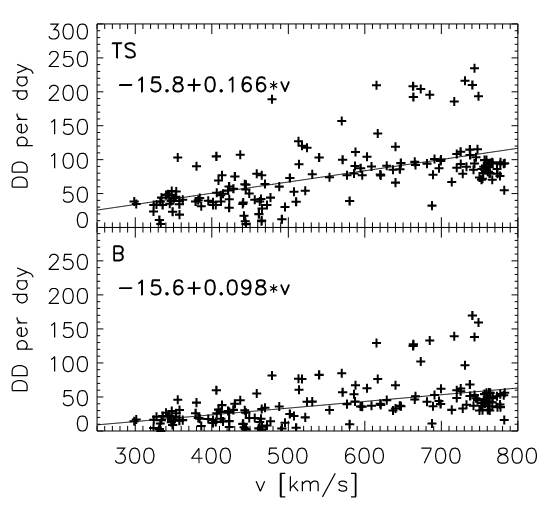
(söding2001?) studied the radial distribution of discontinuities in the solar wind.

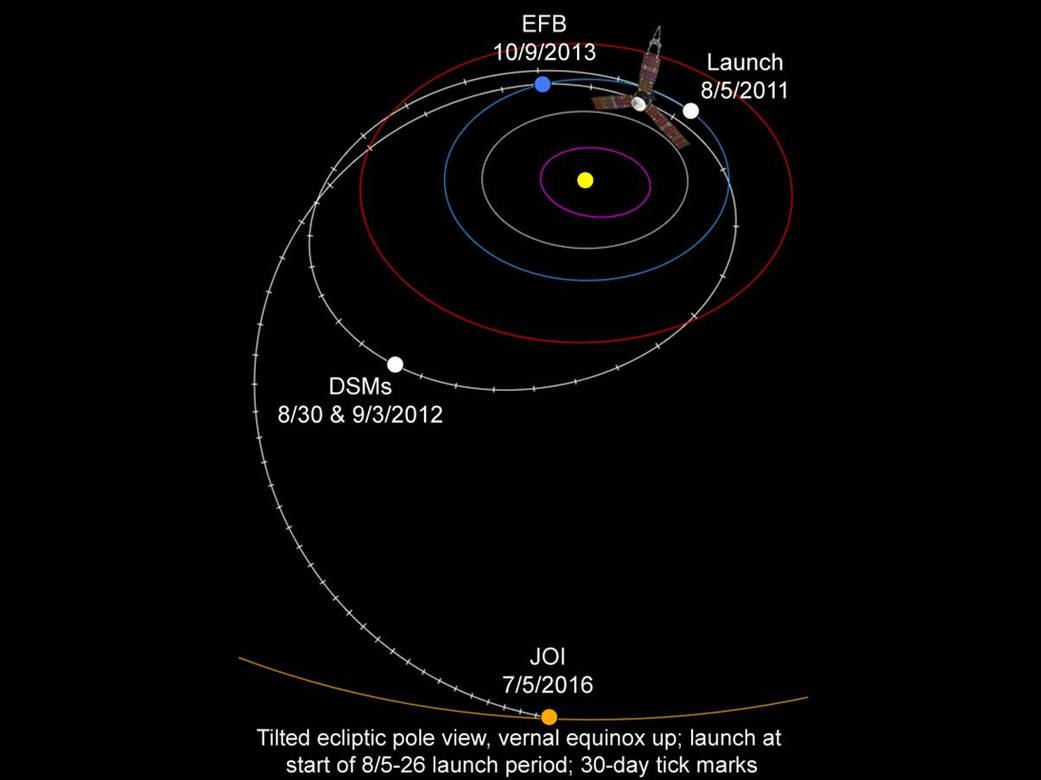
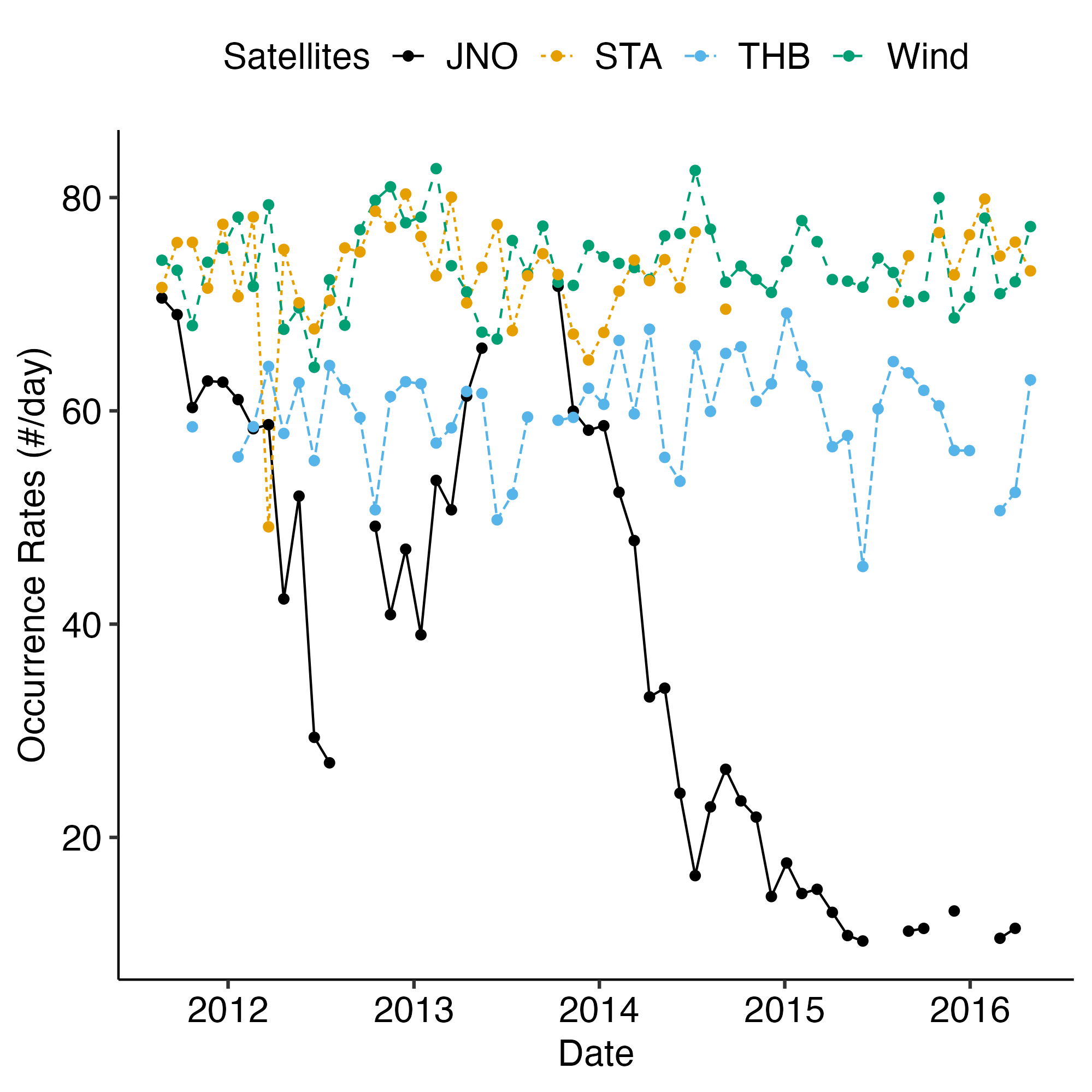
Joint observations of JUNO & ARTEMIS & Other missions really provides a unique opportunity!!!

Method

• We use (liu2022a?) method to identify IDs, which has better compatibility for the IDs with minor field changes.
• Then the minimum variance analysis is applied to each ID event to obtain the boundary normal (LMN) coordinate and extract IDs’ features.
• Hamiltonian model is applied for investigation of ion dynamics in the solar wind discontinuity configuration.

The most generalized form of dimensionless hamiltonian equation for ions in force-free rotational magnetic discontinuities configuration is

\[ H=\frac{1}{2}\left(\frac{1}{6} \alpha^2 c_2 z^3-c_1 z+p_x\right)^2+\frac{p_z^2}{2}+\frac{1}{2}\left(\kappa x-\frac{\alpha z^2}{2}\right)^2 \]

With \(B_l^2+B_m^2=\text { const }\), we have

\[ H=\frac{1}{2}\left(\frac{\alpha^2 z^3}{6 \sqrt{\kappa_m^2+1}}-z \sqrt{\kappa_m^2+1}+p_x\right)^2+\frac{p_z^2}{2}+\frac{1}{2}\left(\kappa_n x-\frac{\alpha z^2}{2}\right)^2 \]

The system has three parameters \[ \kappa_n=\frac{B_n}{B_{l, \max }} \quad \kappa_m=\frac{B_{m, 0}}{B_{l, \max }} \quad \alpha=\frac{l_0}{L}=\frac{\text { gyro radius }}{\text { system length }} \]

Results

Normalized occurrence rate of IDs drops with the radial distance from the Sun, following 1/r law.

• High energy particle has higher chance to cross uncertainty curve
• High shear magnetic field will make separatrix vanishes and the geometrical jumps of the quasiadiabatic invariant disappear