Solar Wind Discontinuities: Parker Solar Probe vs ARTEMIS Observations
SPARTHB
Solar wind discontinuities (SWD)
Discontinuous changes in plasmas parameters and magnetic fields
Import element of solar wind turbulences
Very kinetic structure: interact with energetic part of the solar wind ions
Formation of SWD
Turbulent ion heating by reconnection of tangential discontinuities. (a) Current density (color) and magnetic field lines, possible reconnection sites are indicated by crosses. (b) The proton temperature anisotropy (color) that indicates acceleration
Alfven wave steepening results in the discontinuity formation: magnetic energy transport from large scale (Alfven waves generated in the solar corona) to small (ion kinetic) scales of discontinuities, where this energy can be dissipated to particle heating
Motivation
Studying the radial evolution of solar wind discontinuities from synergistic observations of PSP and Earth-orbiting missions (ARTEMIS, Wind) during aligned intervals.
How does the discontinuities change with the radial distance from the Sun?
How is solar wind discontinuities formed? What is the physical mechanisms?
Generated at or near the sun?
Locally generated in the interplanetary space by turbulence?
In-situ synergistic observations
Similar type of solar wind or Same solar solar wind
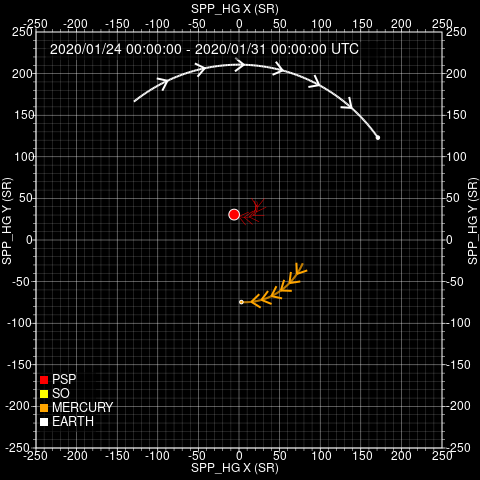
How to define alignment?
Trajectory & Orbits (theory): ballistic approximation of Parker spiral
Plasma properties (observation):
Invariants: plasma composition, ionization states, mass flux \(n u r^2\)
Correlation: magnetic field / plasma velocity
Simulation: Trace plasma parcels evolution
Orbits
ENLIL simulation
Normalized solar wind density at the ecliptic and the IMF lines
Radial solar wind velocity at the ecliptic on the global and detail regions together with the temporal profile at spacecraft
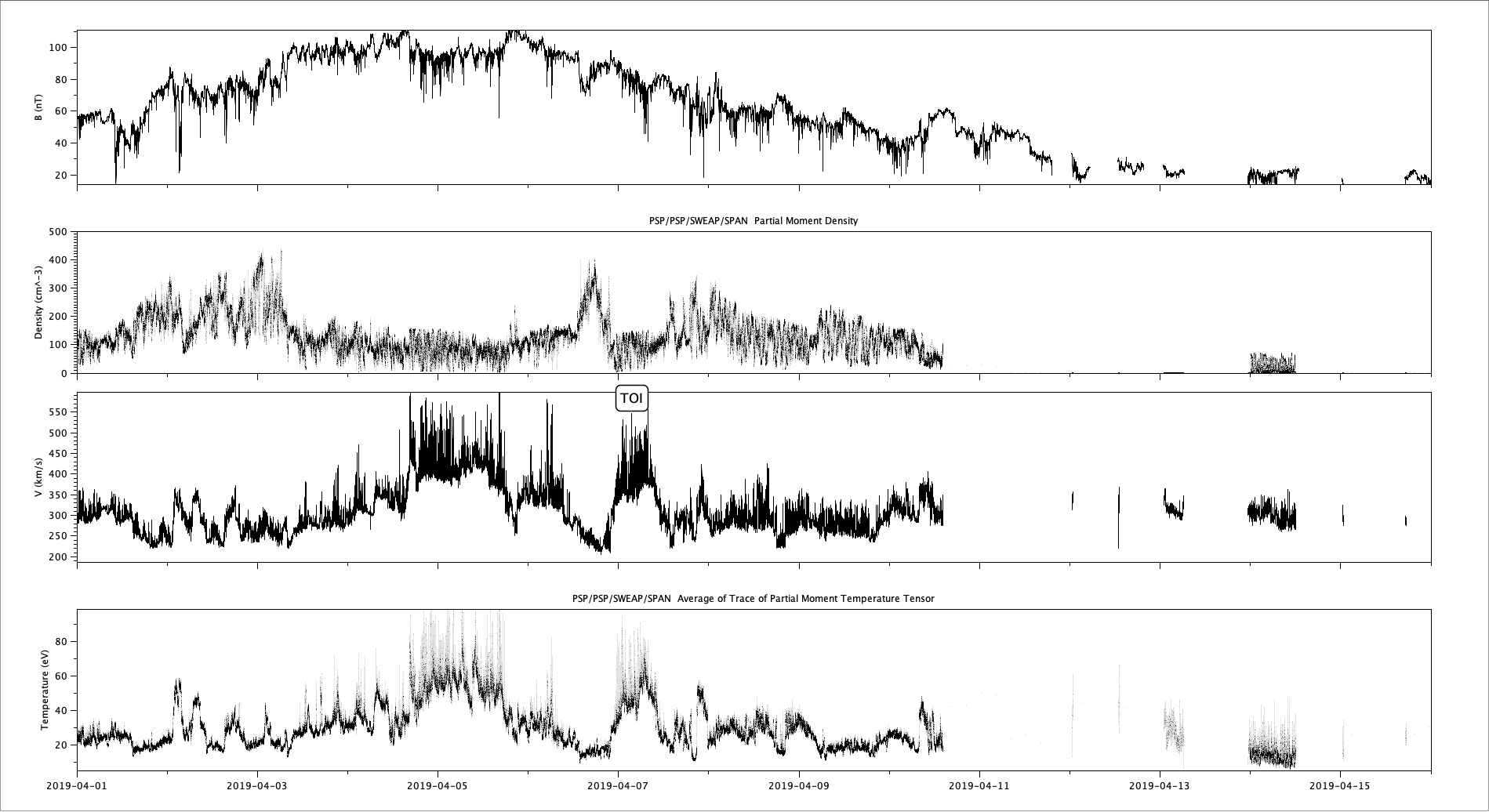
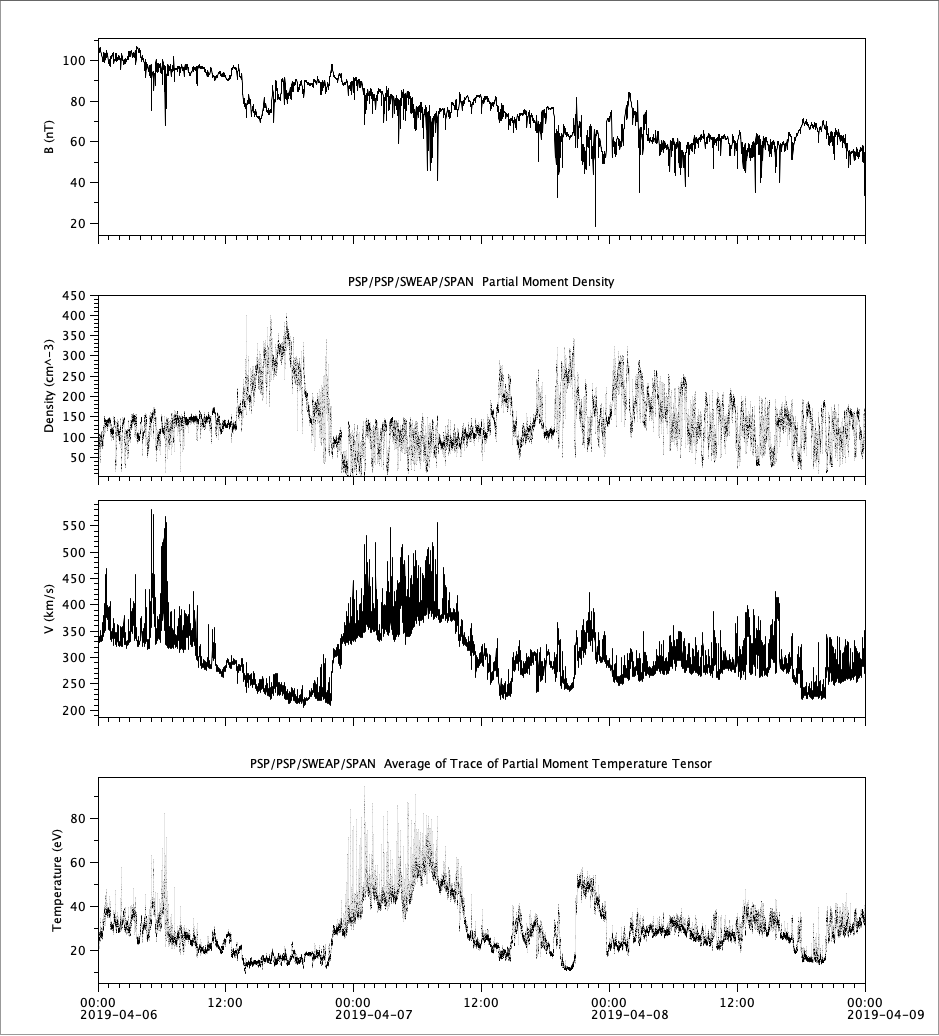
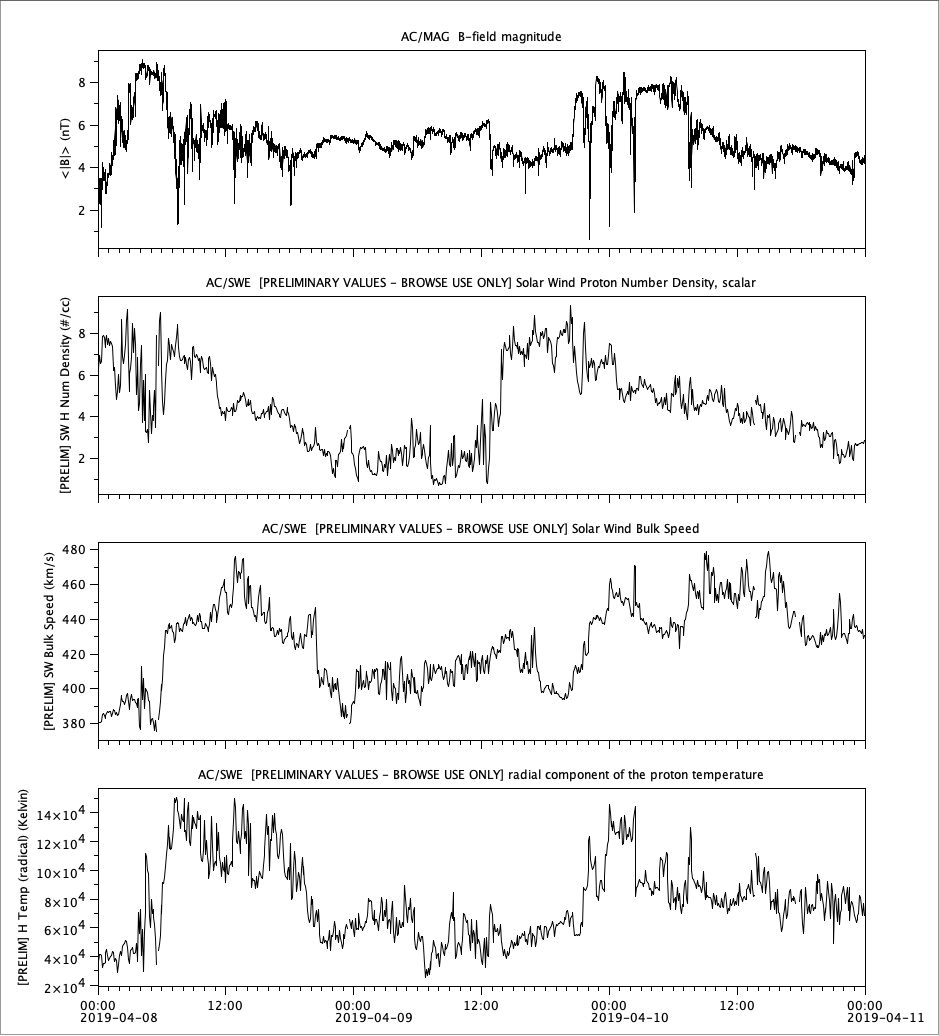
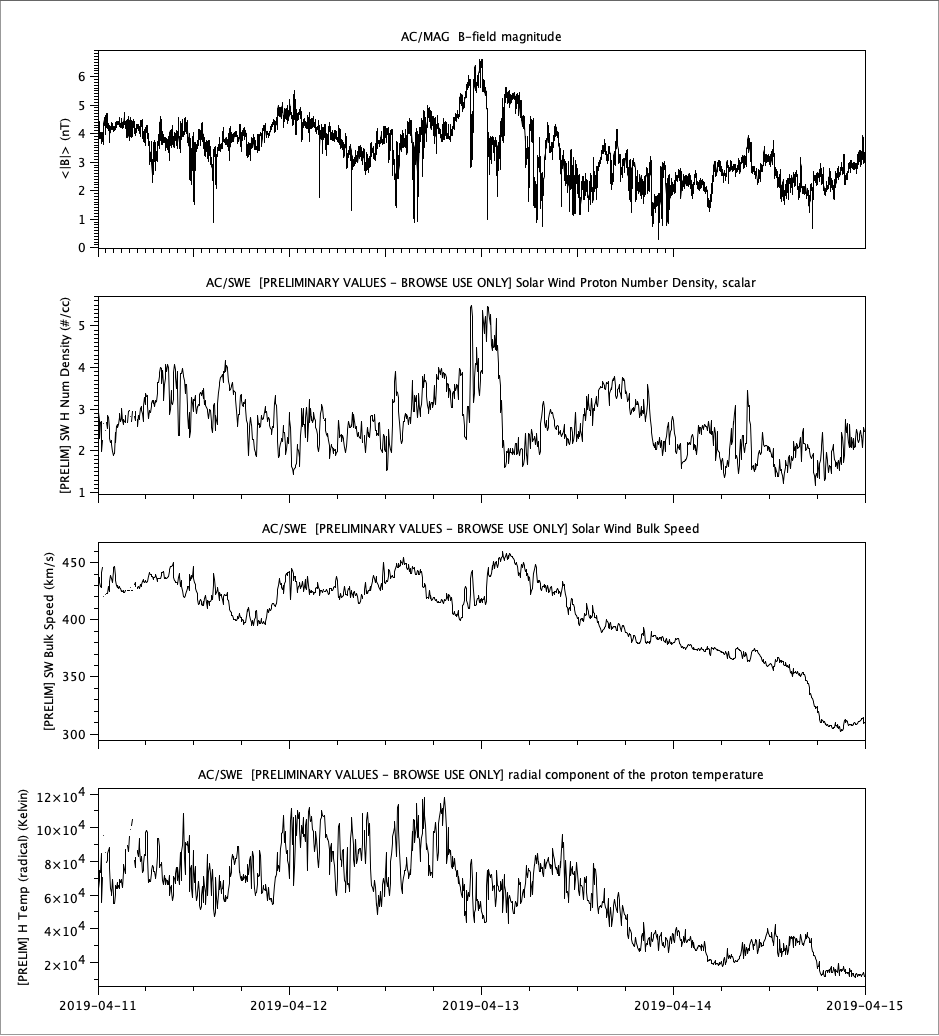
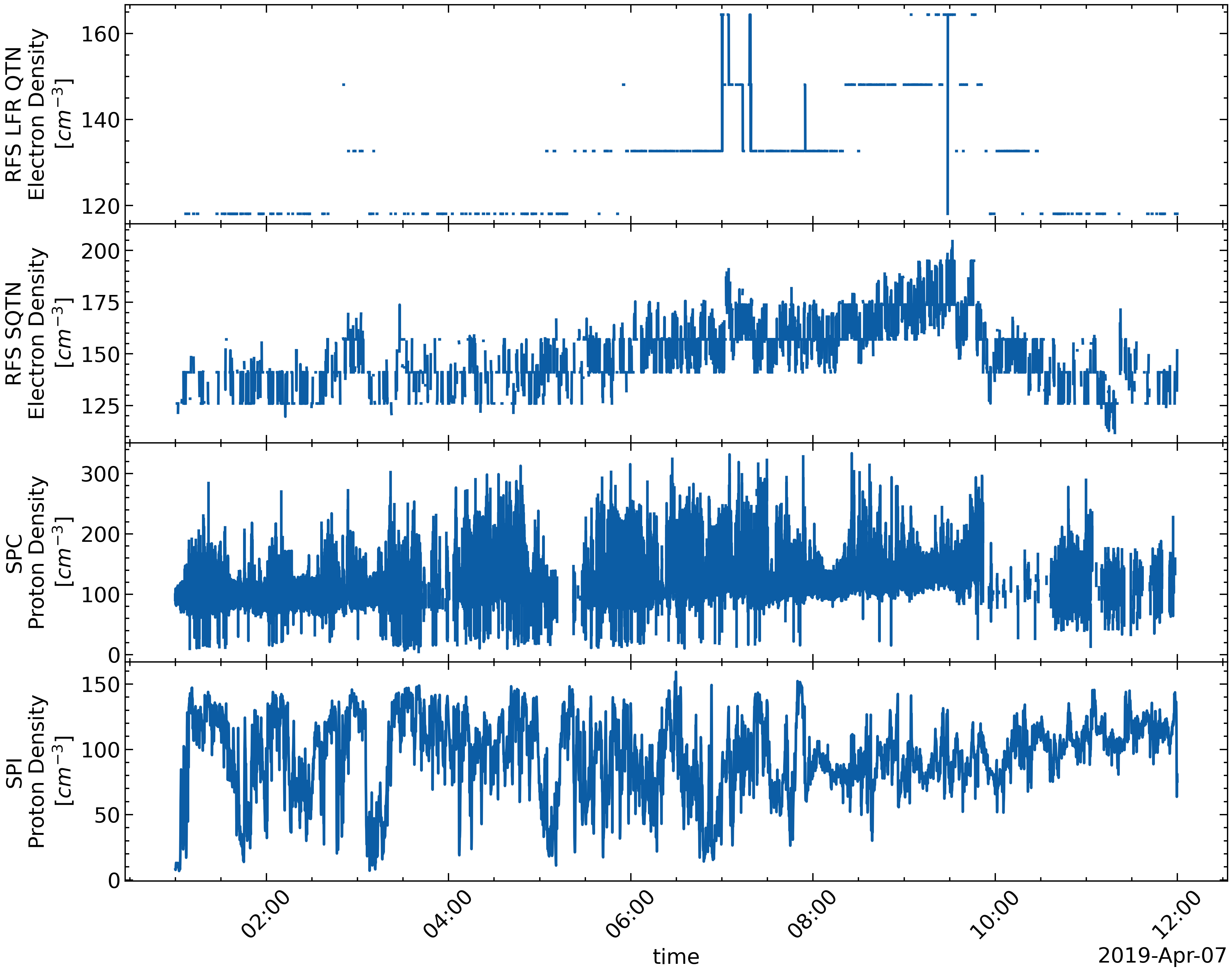
Observation
Observation (continued)
Time resolution (from high to low): SPC, SPI, SQTN, QTN
Quality (fluctuating, from high to low): SQTN, QTN, SPC/SPI
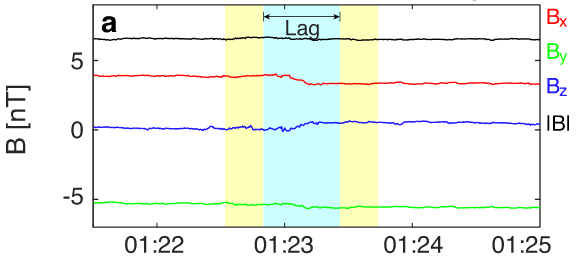
Examples of discontinuities
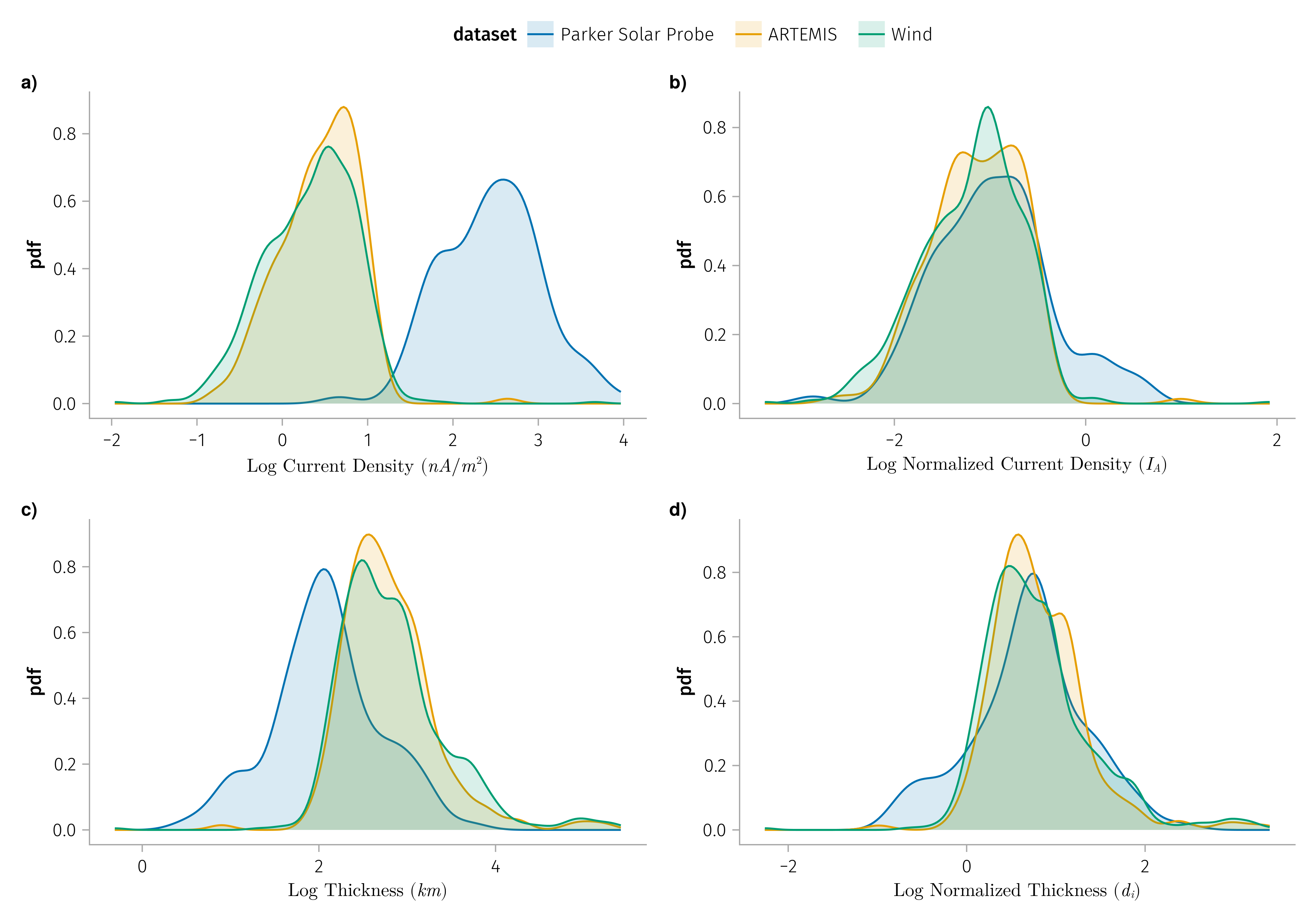
In general discontinuities observed by PSP are with
shorter duration (1~5 secs)
compared with 5-10 secs
large current density (100-1000 nA/m^2)
compared with 1-10 nA/m^2
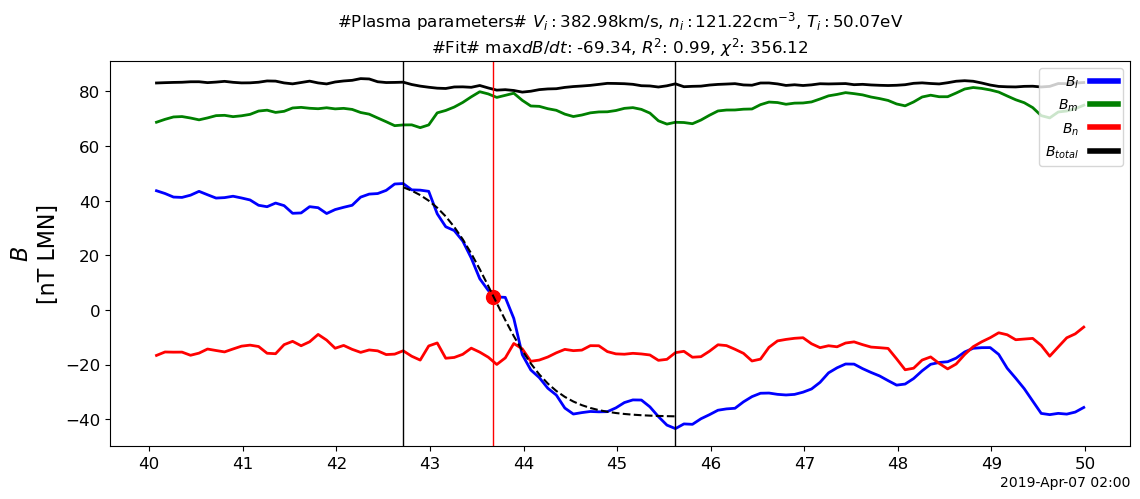
Identification/Detection method
Liu et al. (2022)
Compared with adjacent intervals without sampling
Properties of discontinuities
Every discontinuity’s \(l\) component is fitted by a \(\tanh\) (logistic) function.
Combined with plasma data (\(n\), \(v\), \(T\))
\(L\): thickness of the discontinuity
\(J_0\): maxium current density
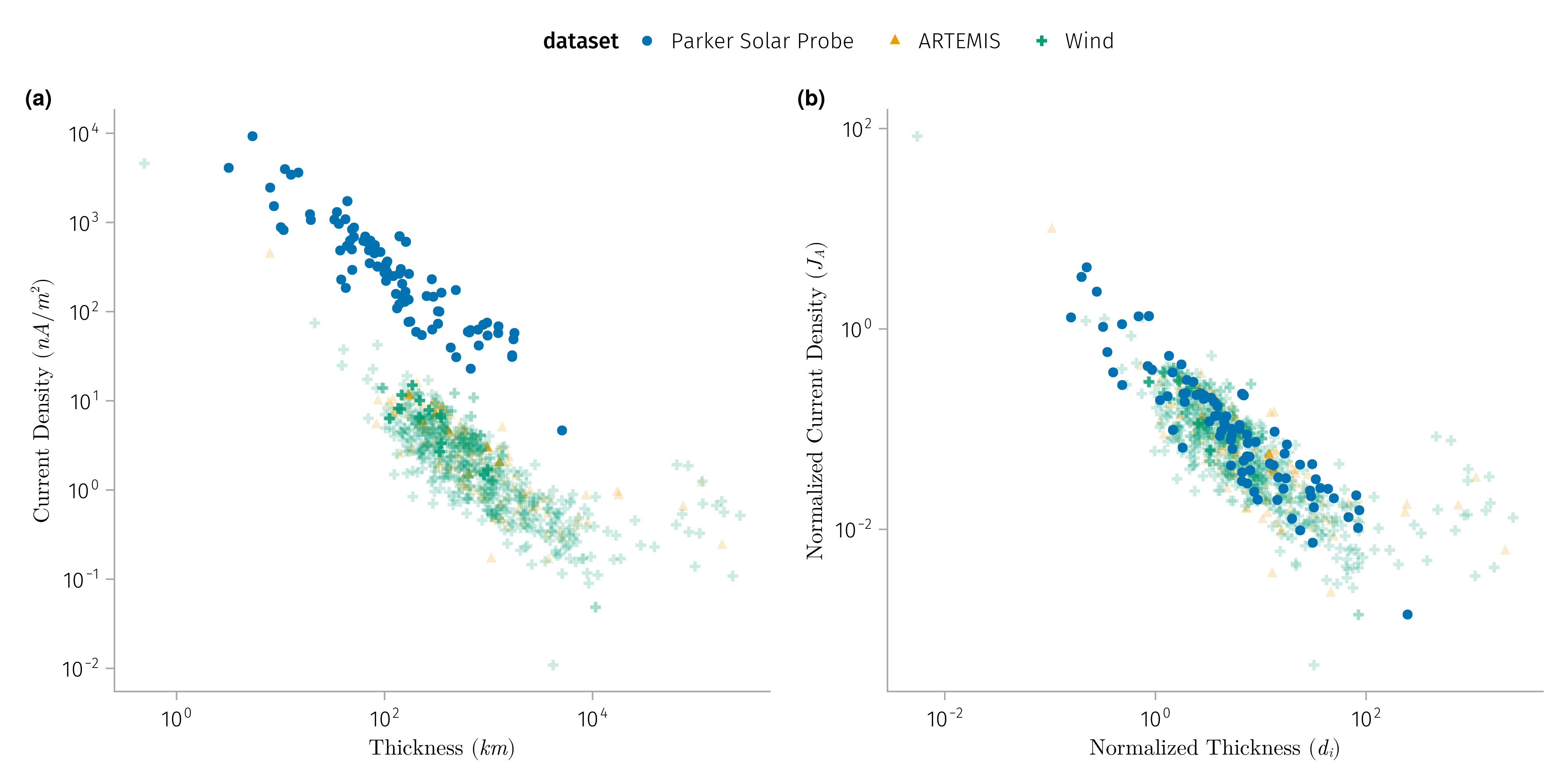
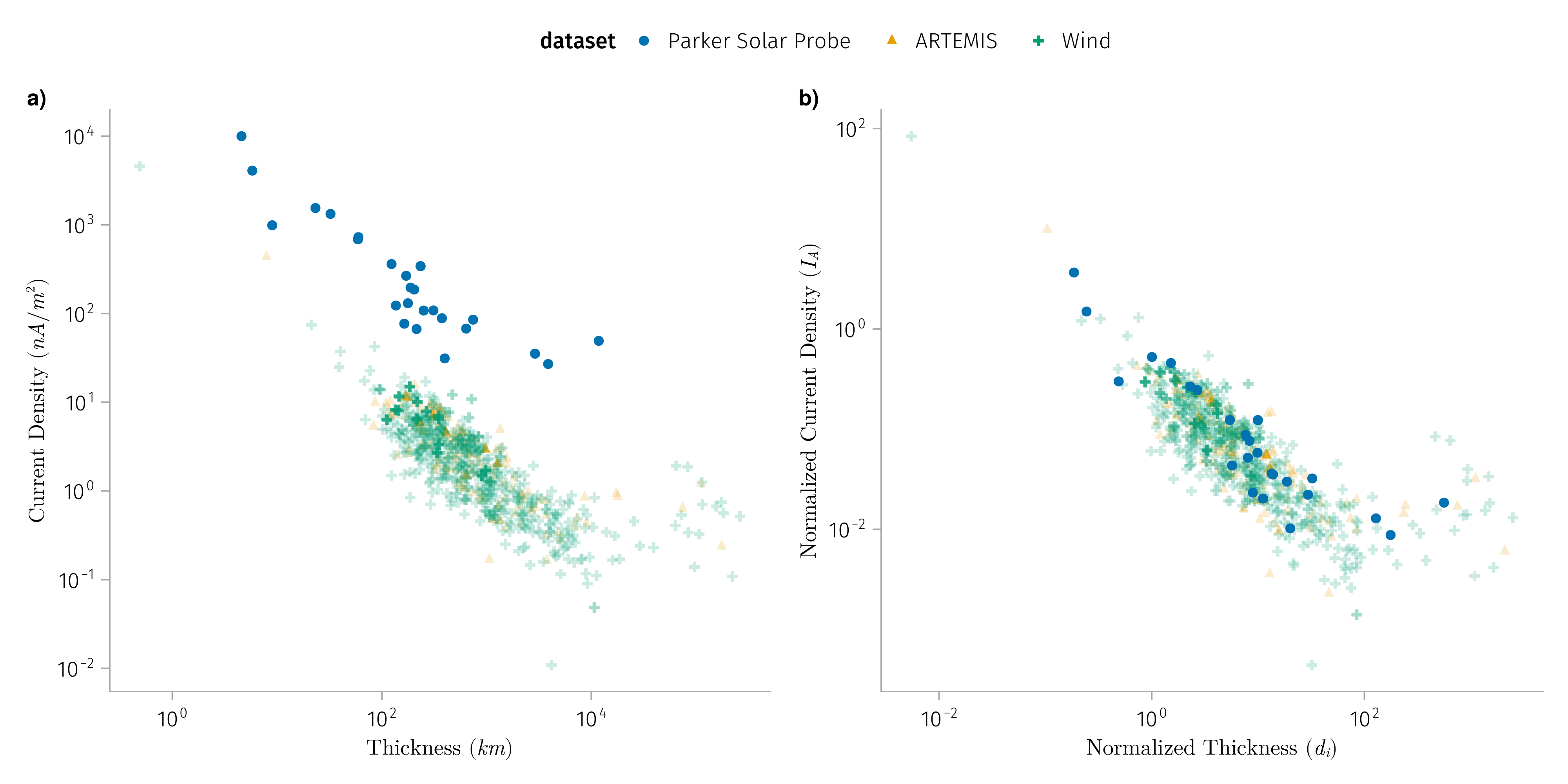
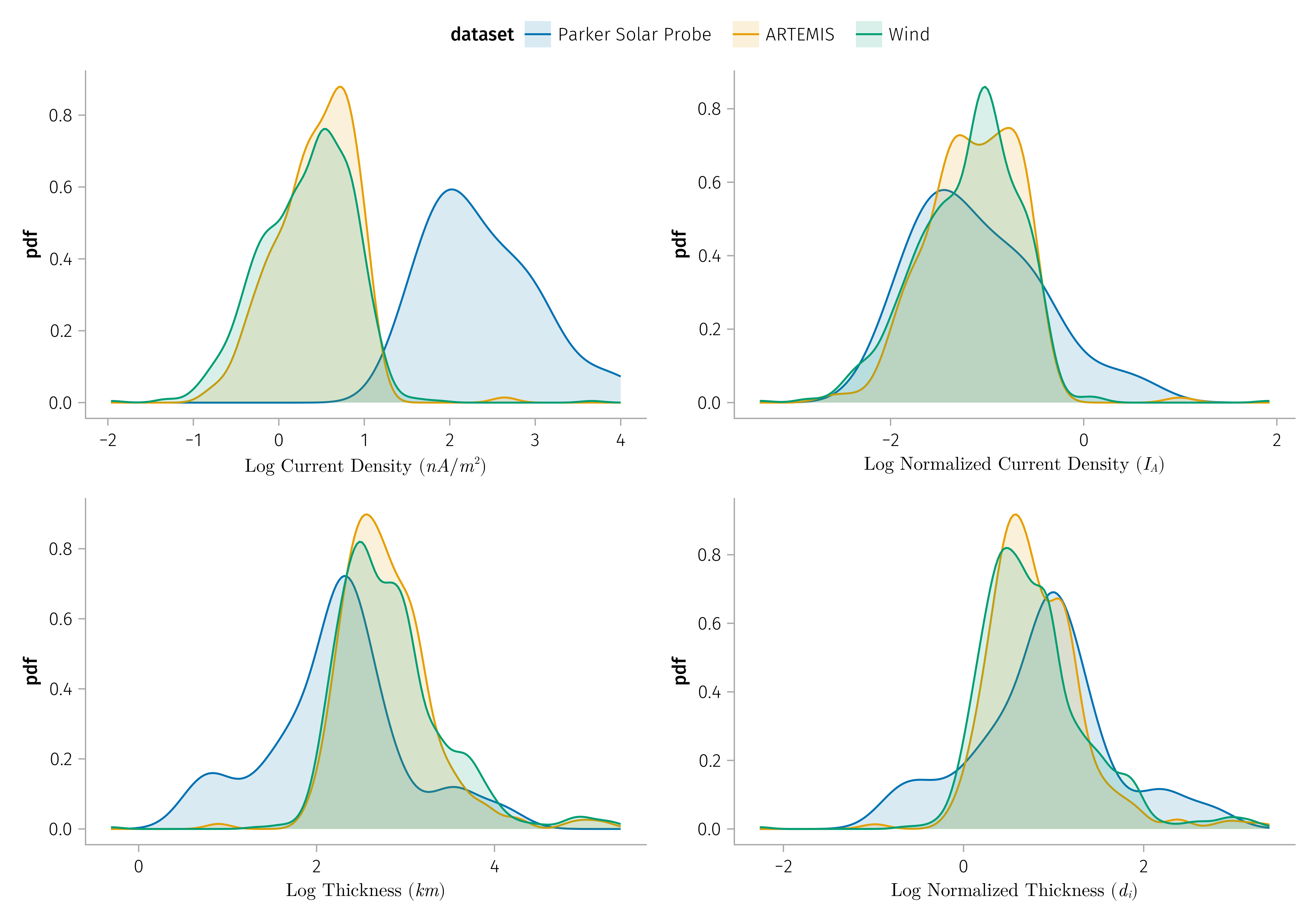
If we expect the discontinuities to be generated locally, then the thickness of the discontinuities should be related to local plasma parameters:
- Normalize thickness by \(d_i\) (ion inertial length) or \(r_i\) (ion gyroradius)
- Normalize current density by \(J_A\) (Alfven current density)
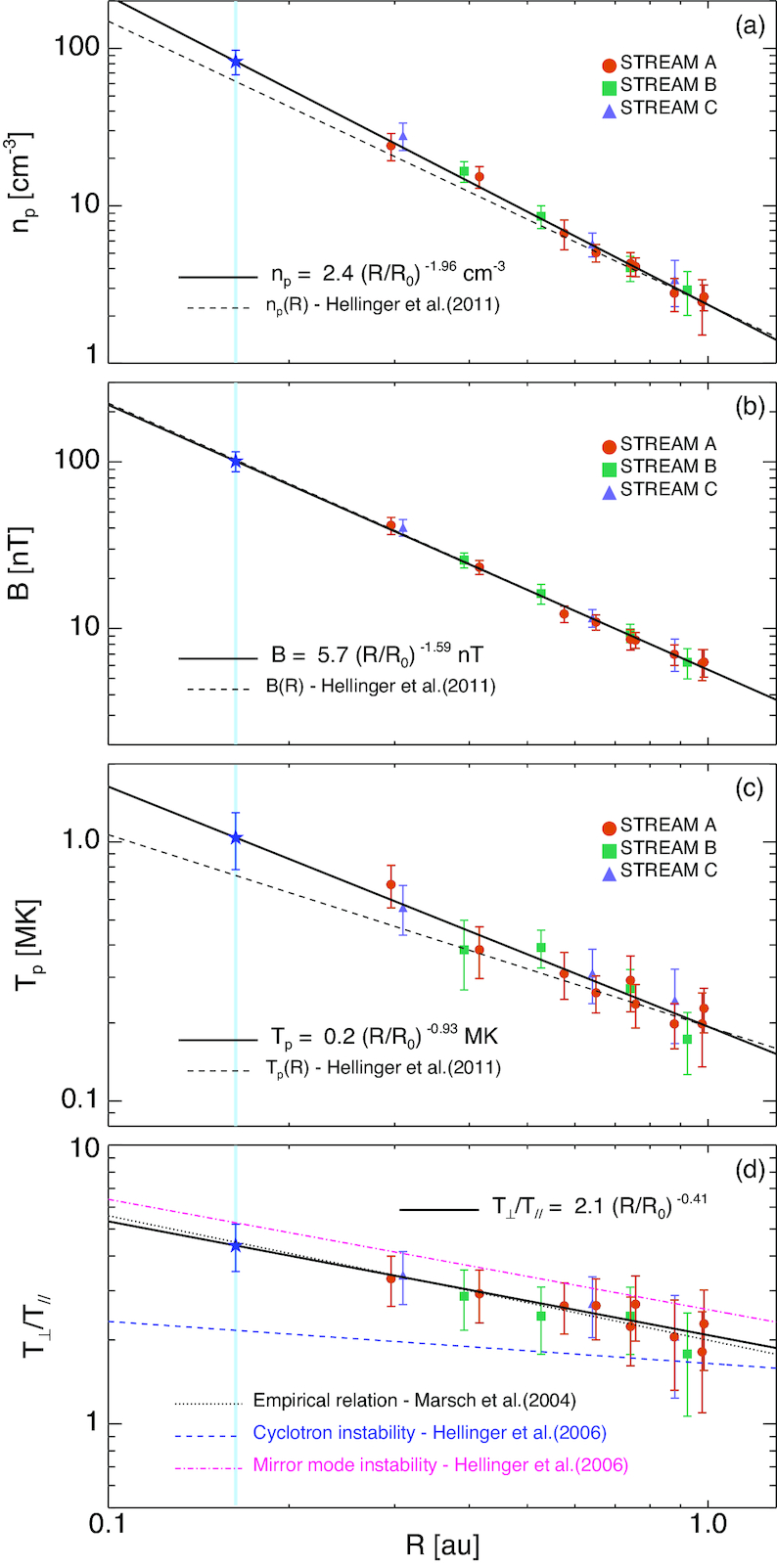
Plasma adiabatic evolution
Perrone et al. (2019)
Comparison with discontinuities properties
K1: Normalized discontinuities properties does not vary much with radial distance
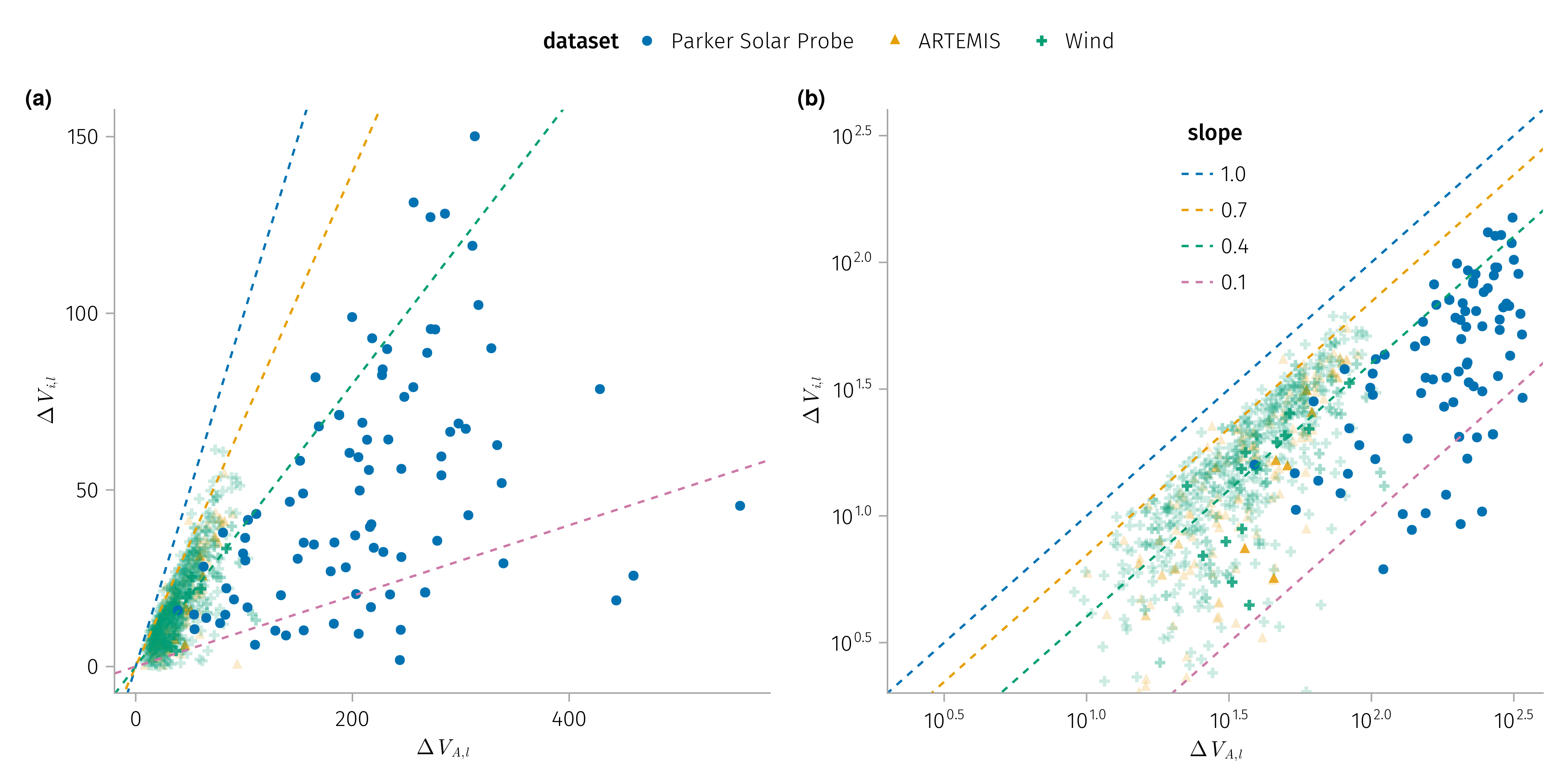
K2: \(Δv_l\),l demonstrates a strong correlation with \(Δv_{A}\), albeit being consistently smaller.
Comparison with Alfven speed and plasma speed change
For rotational discontinuities, the plasma velocity jump across them: the plasma flow velocity \(v_l\) (the solar wind velocity projected onto \(l\)) changes due to changes in \(B_l\), \(Δv_l=±Δv_A\) with \(v_A= B_l / \sqrt{4 n m}\) (Hudson 1970).
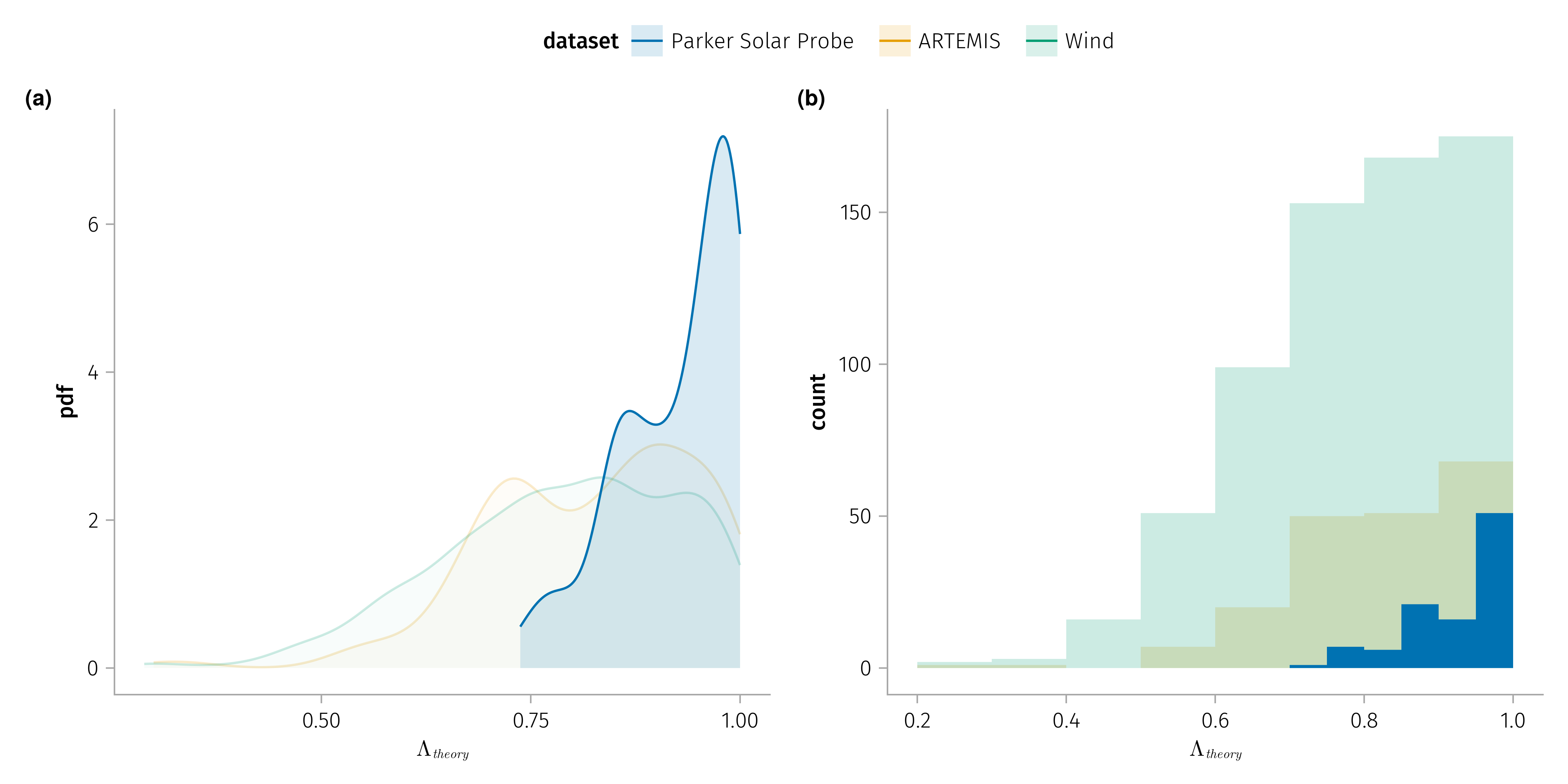
Comparison with anisotropy
The equation for \(Δv_A\) includes a factor depending on the anisotropy of the plasma.
Pressure anisotropy \(Λ = \mu (P_∥ - P_⊥) / B^2\).
Conclusion
- The properties of the discontinuities is related to the local plasma parameters
- Thickness => ion inertial length
- Current density => Alfven velocity (current density)
- Normalized thickness and current density of discontinuities remain constant with radial distance
- Anisotropy of the plasma is expected to be larger near the sun to explain the observed speed change ratio \(Δv_i/Δv_A\).