Solar Wind Discontinuities: Parker Solar Probe vs ARTEMIS Observations

SPARTHB

Zijin Zhang
Anton V. Artemyev
Vassilis Angelopoulos
Chen Shi
Zesen Huang

2024-03-01

Solar wind discontinuities (SWD)

Discontinuous changes in plasmas parameters and magnetic fields

  • Import element of solar wind turbulences

  • Very kinetic structure: interact with energetic part of the solar wind ions

Formation of SWD

Turbulent ion heating by reconnection of tangential discontinuities. (a) Current density (color) and magnetic field lines, possible reconnection sites are indicated by crosses. (b) The proton temperature anisotropy (color) that indicates acceleration

Alfven wave steepening results in the discontinuity formation: magnetic energy transport from large scale (Alfven waves generated in the solar corona) to small (ion kinetic) scales of discontinuities, where this energy can be dissipated to particle heating

Motivation

Studying the radial evolution of solar wind discontinuities from synergistic observations of PSP and Earth-orbiting missions (ARTEMIS, Wind) during aligned intervals.

  • How does the discontinuities change with the radial distance from the Sun?

  • How is solar wind discontinuities formed? What is the physical mechanisms?

    • Generated at or near the sun?

    • Locally generated in the interplanetary space by turbulence?

In-situ synergistic observations

Similar type of solar wind or Same solar solar wind

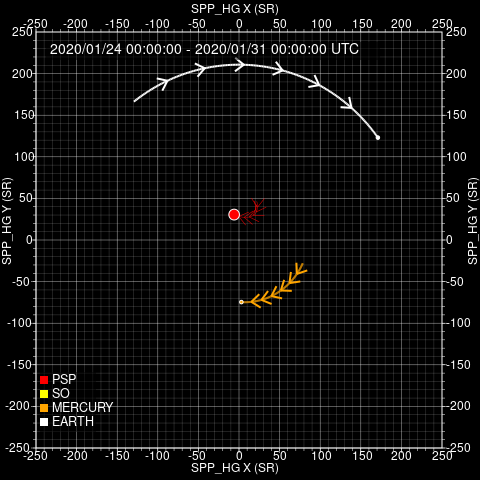
How to define alignment?

  • Trajectory & Orbits (theory): ballistic approximation of Parker spiral

  • Plasma properties (observation):

    • Invariants: plasma composition, ionization states, mass flux \(n u r^2\)

    • Correlation: magnetic field / plasma velocity

  • Simulation: Trace plasma parcels evolution

Orbits

Heliographic frame (corotating with Sun)

ENLIL simulation

Normalized solar wind density at the ecliptic and the IMF lines

Radial solar wind velocity at the ecliptic on the global and detail regions together with the temporal profile at spacecraft

Observation

PSP Observation Overvall

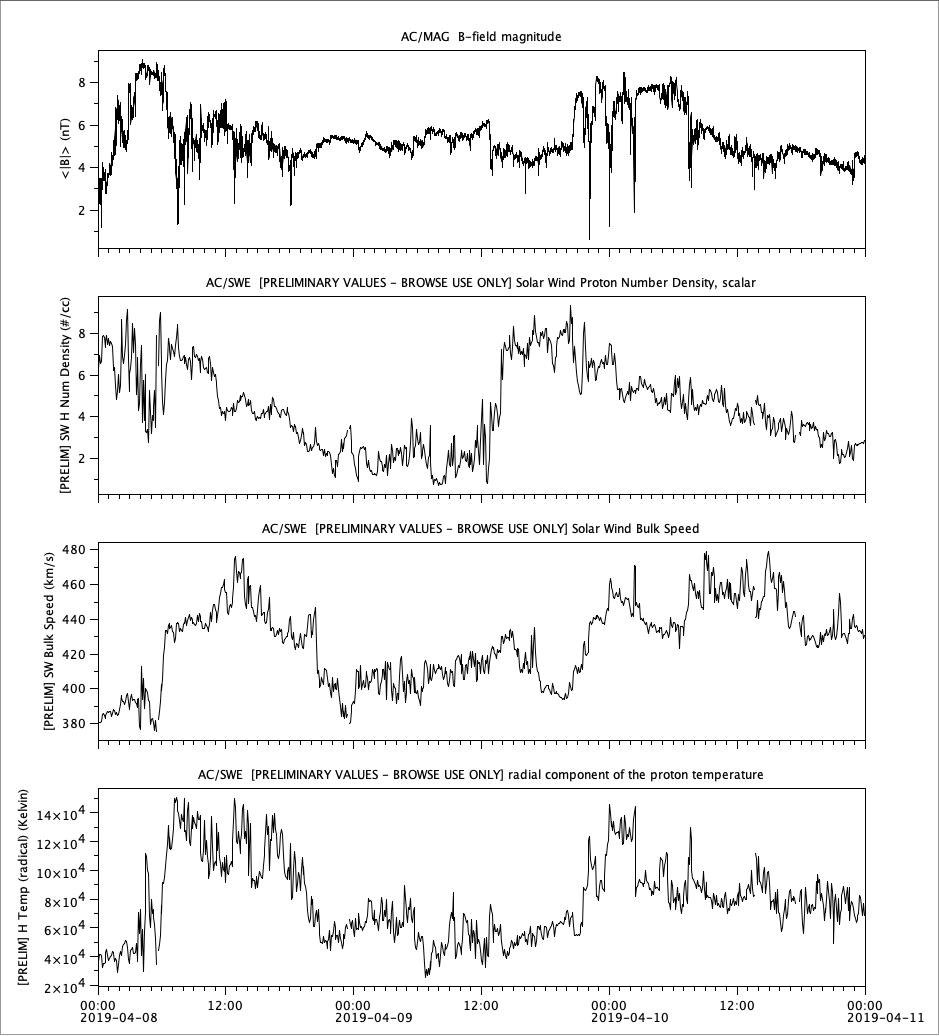
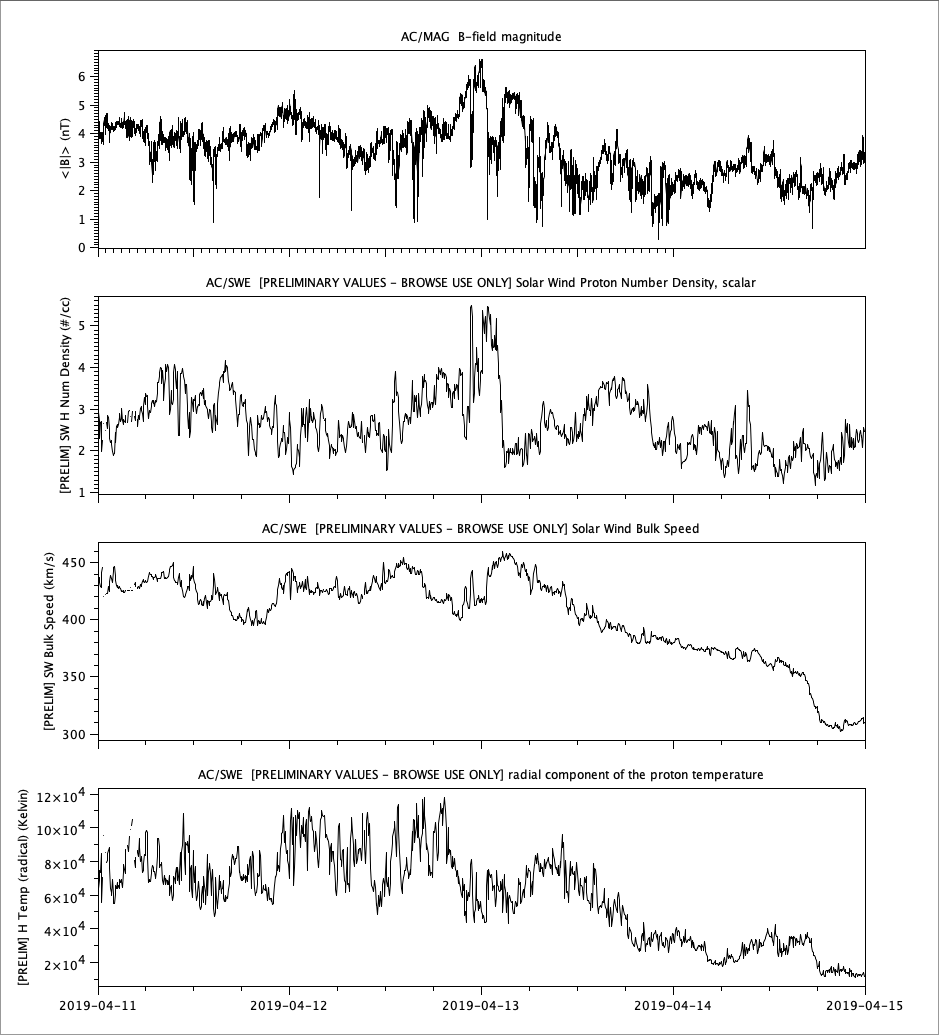
PSP observation

Observation (continued)

PSP observation

ACE observation

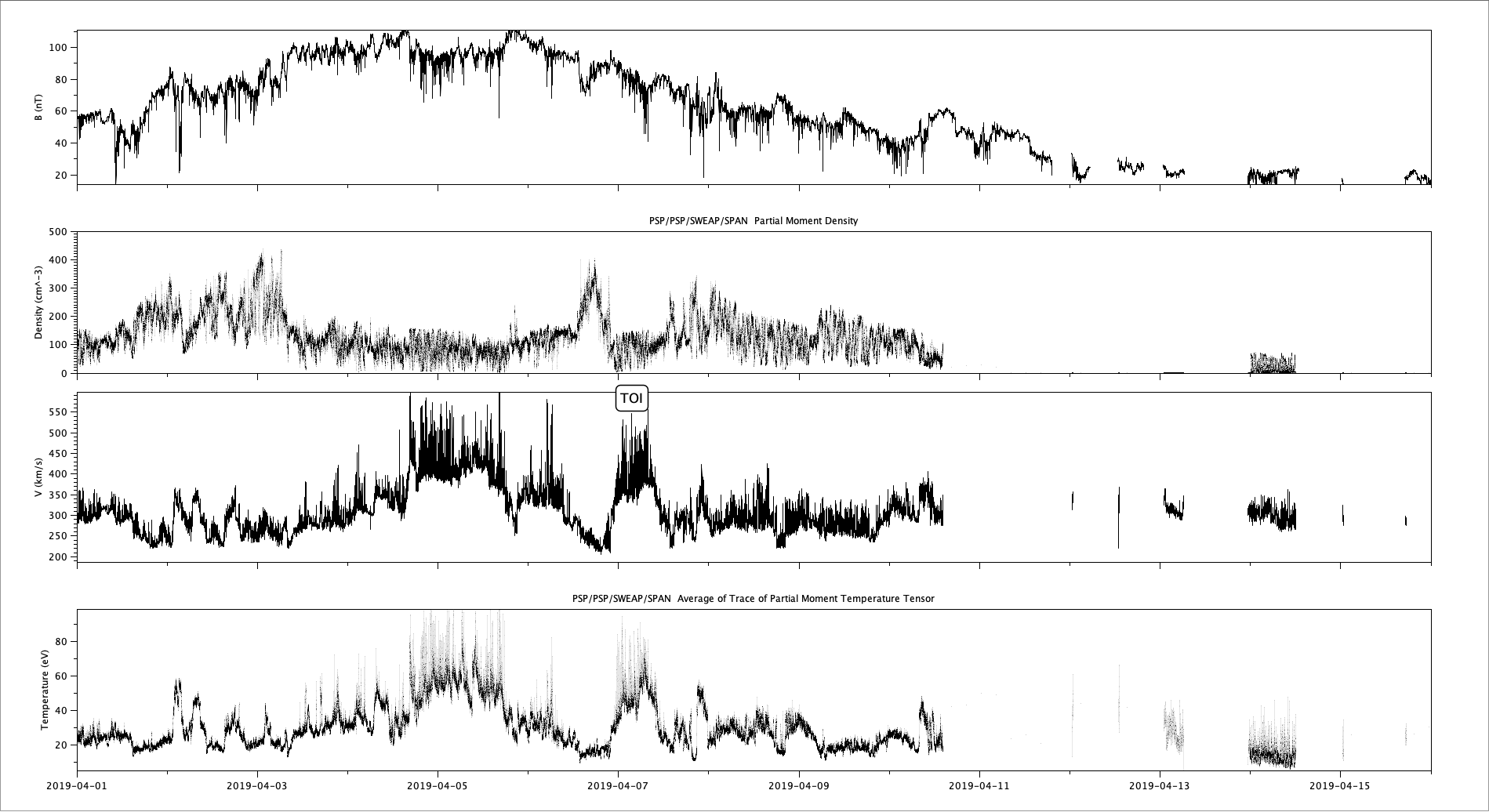
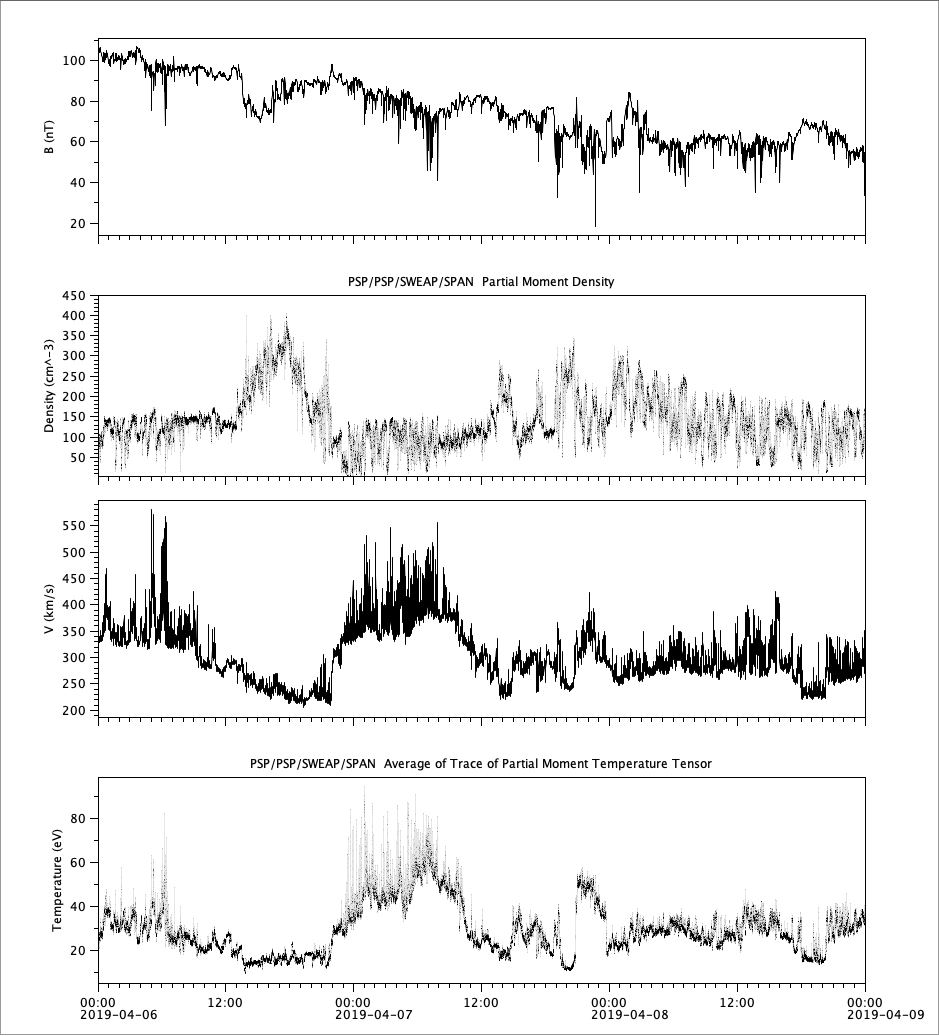
ACE observation (continued)

Time resolution (from high to low): SPC, SPI, SQTN, QTN

Quality (fluctuating, from high to low): SQTN, QTN, SPC/SPI

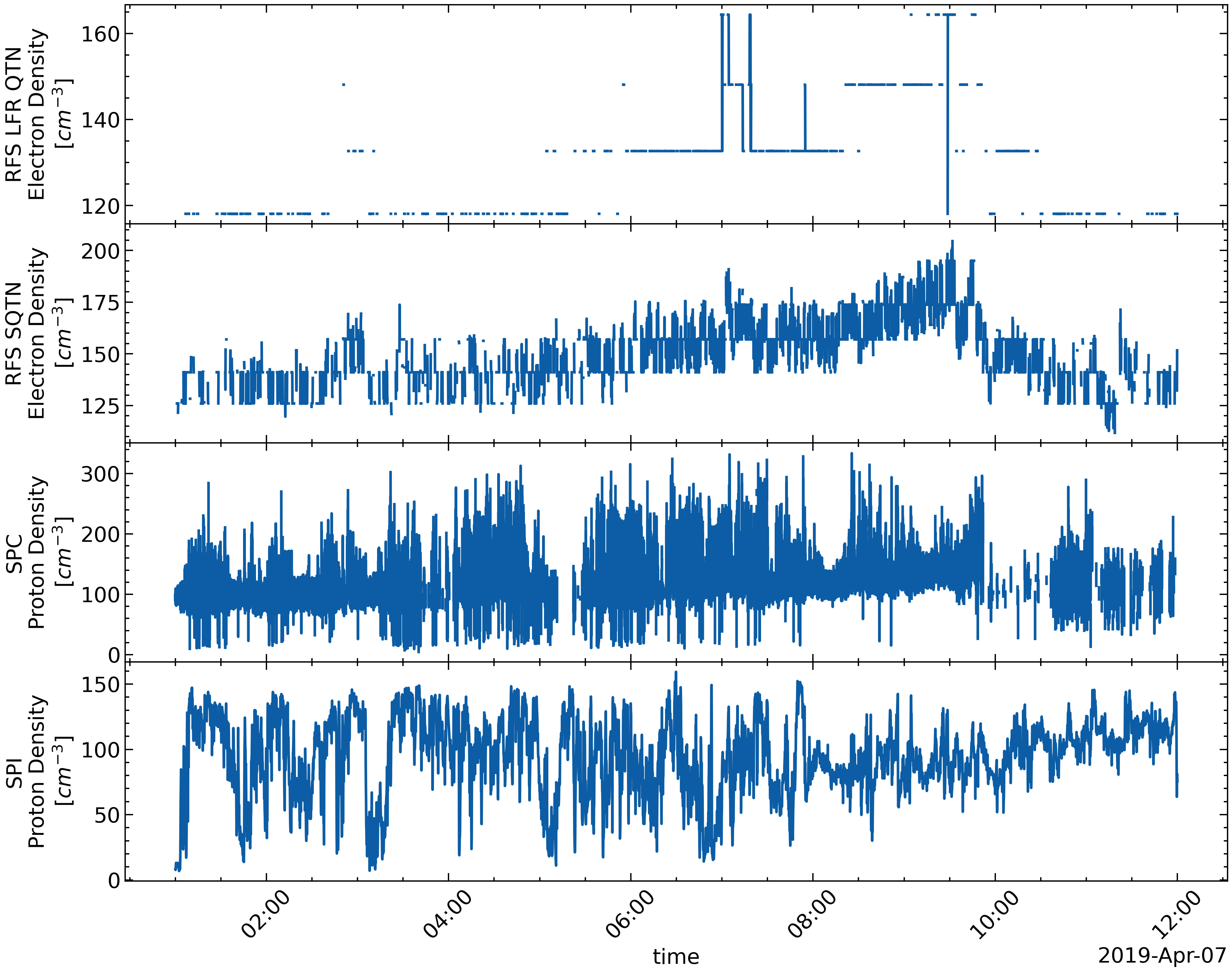
Different Density Product

Examples of discontinuities

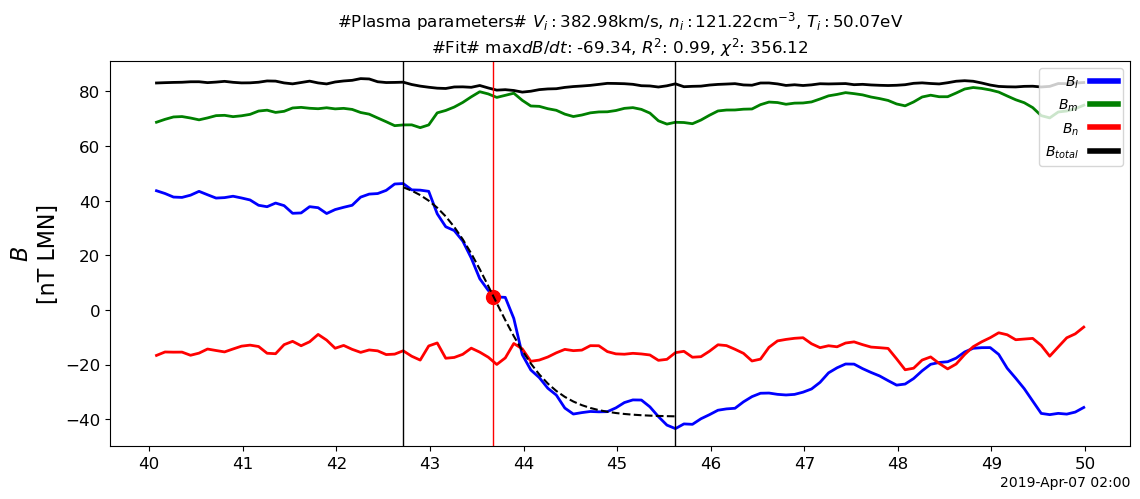
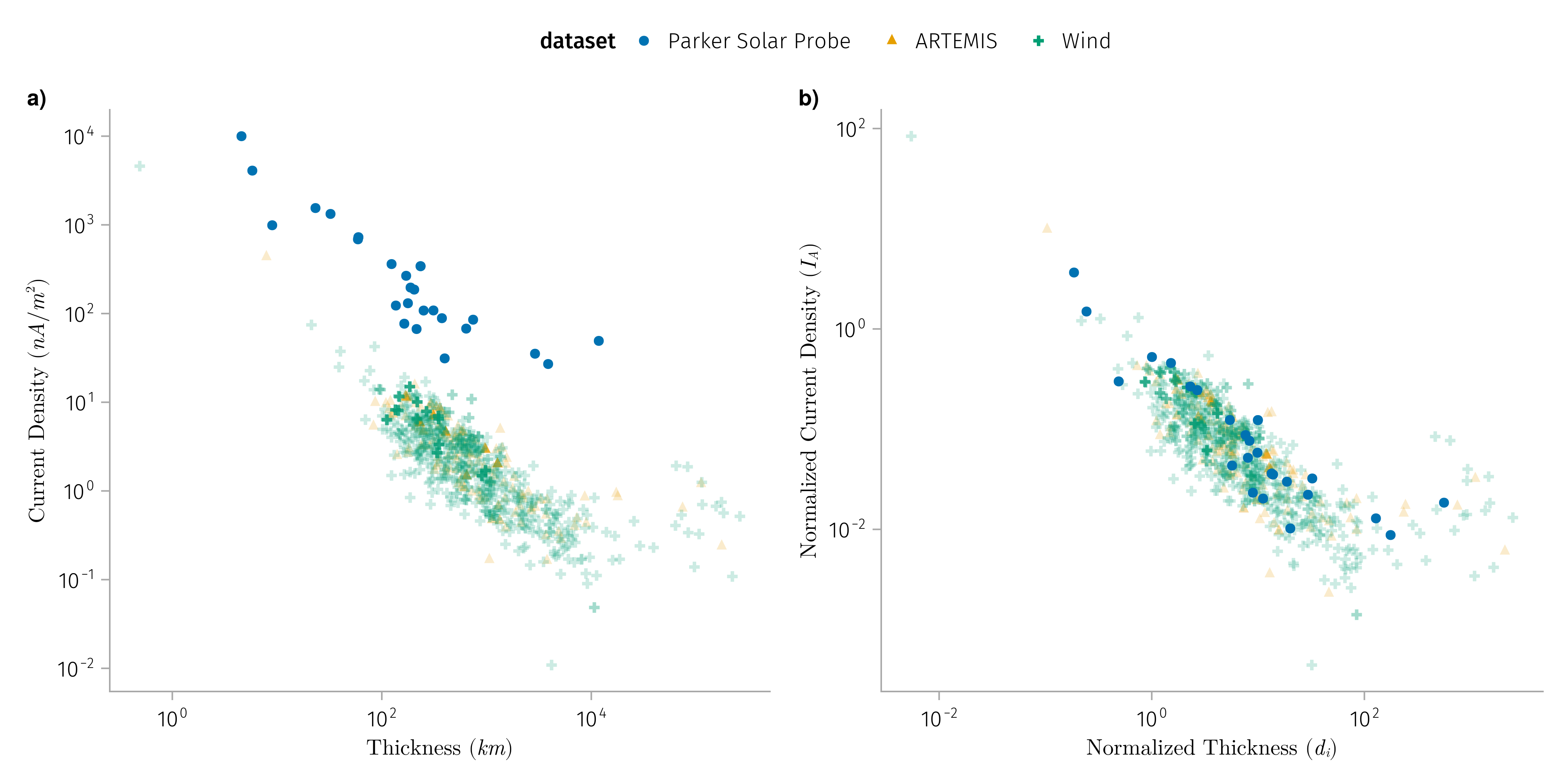
In general discontinuities observed by PSP are with

  • shorter duration (1~5 secs)

    compared with 5-10 secs

  • large current density (100-1000 nA/m^2)

    compared with 1-10 nA/m^2

Identification/Detection method

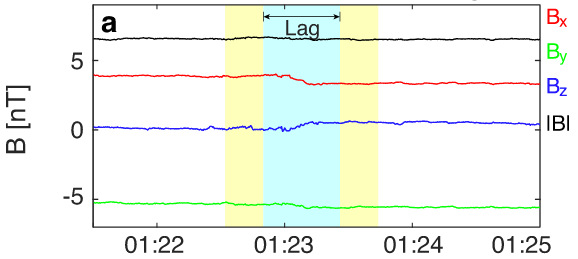
Liu et al. (2022)

Compared with adjacent intervals without sampling

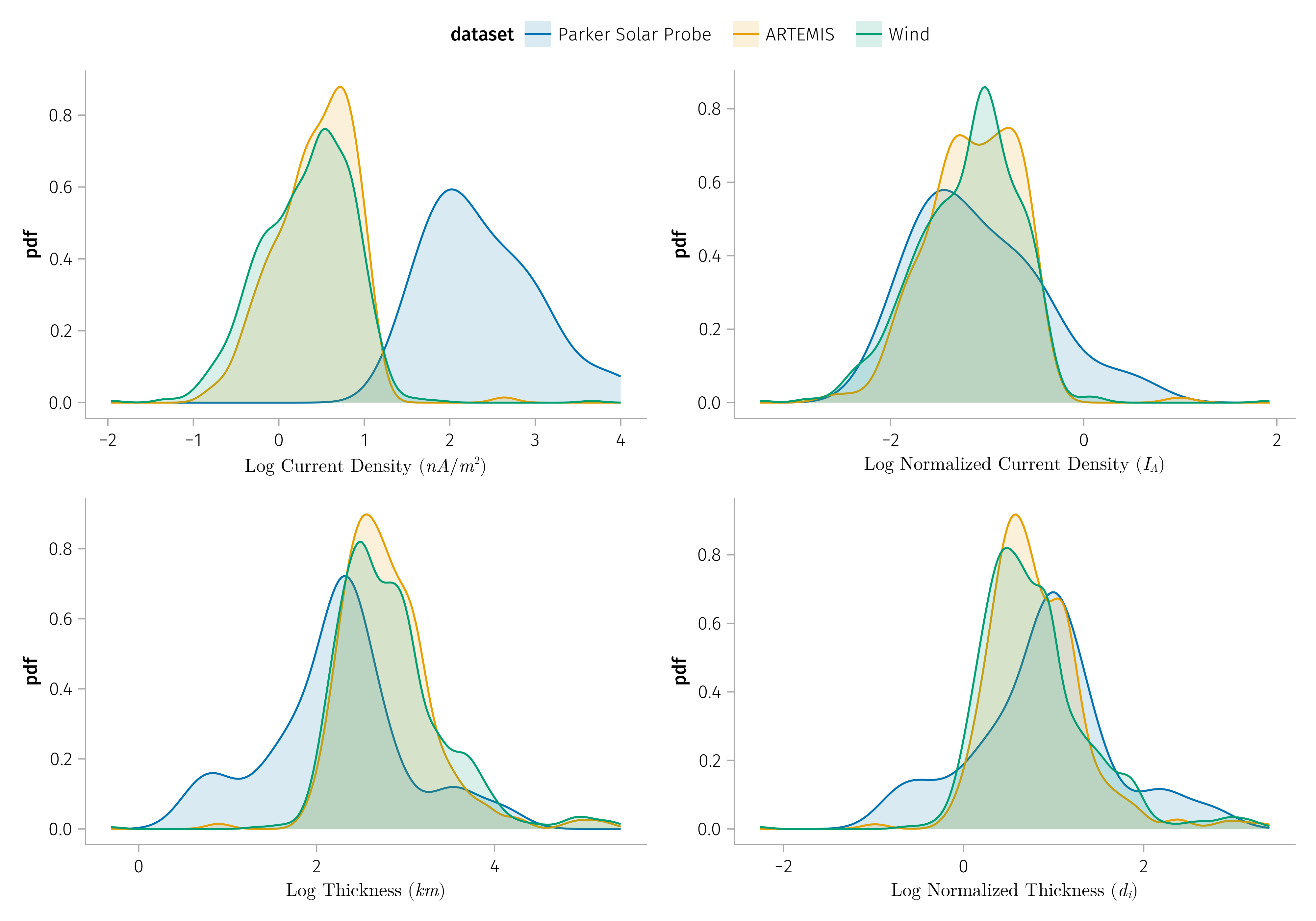
Properties of discontinuities

Every discontinuity’s \(l\) component is fitted by a \(\tanh\) (logistic) function.

Combined with plasma data (\(n\), \(v\), \(T\))

\(L\): thickness of the discontinuity

\(J_0\): maxium current density

If we expect the discontinuities to be generated locally, then the thickness of the discontinuities should be related to local plasma parameters:

  • Normalize thickness by \(d_i\) (ion inertial length) or \(r_i\) (ion gyroradius)
  • Normalize current density by \(J_A\) (Alfven current density)

Plasma adiabatic evolution

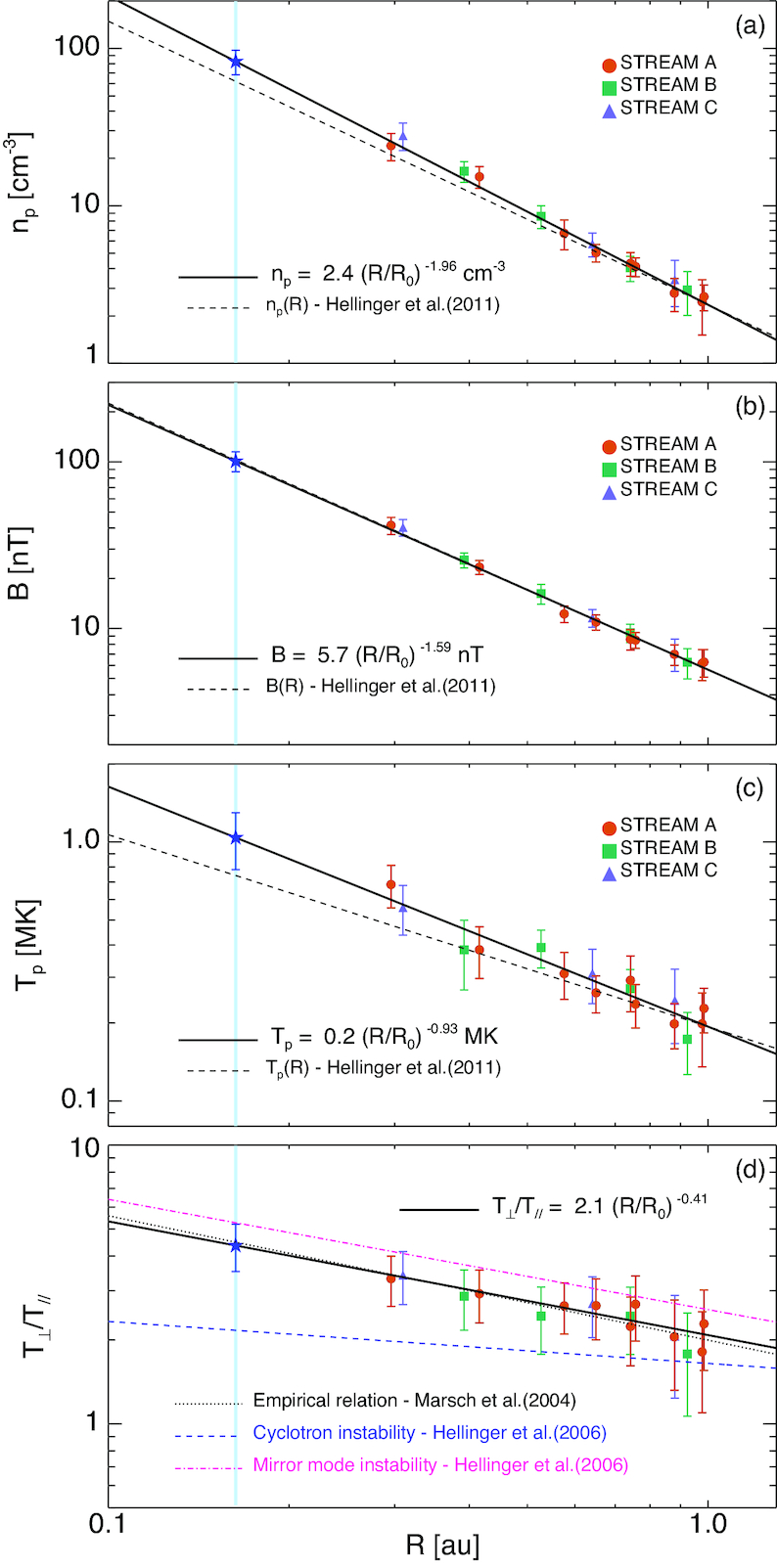
Perrone et al. (2019)

Comparison with discontinuities properties

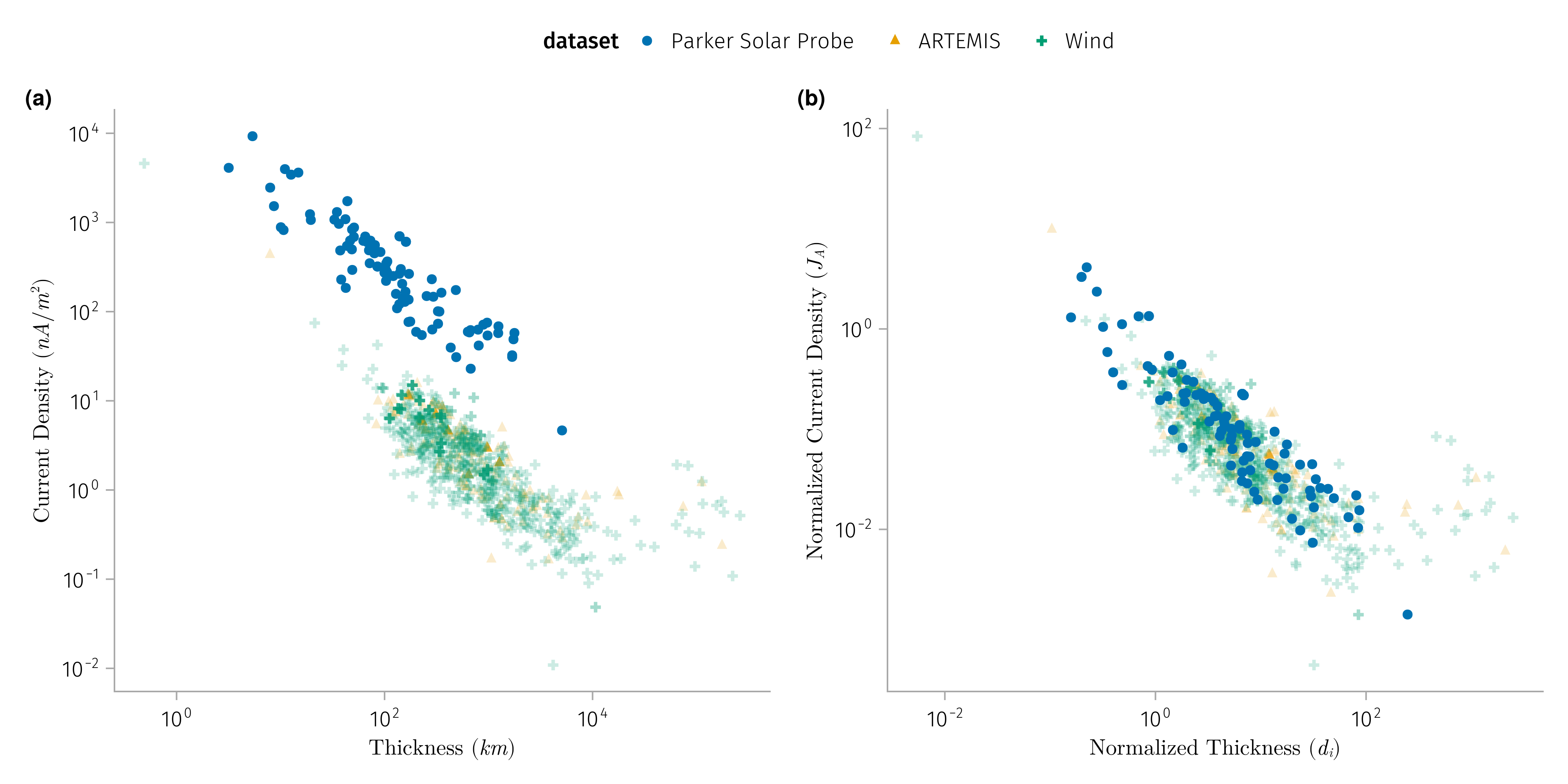
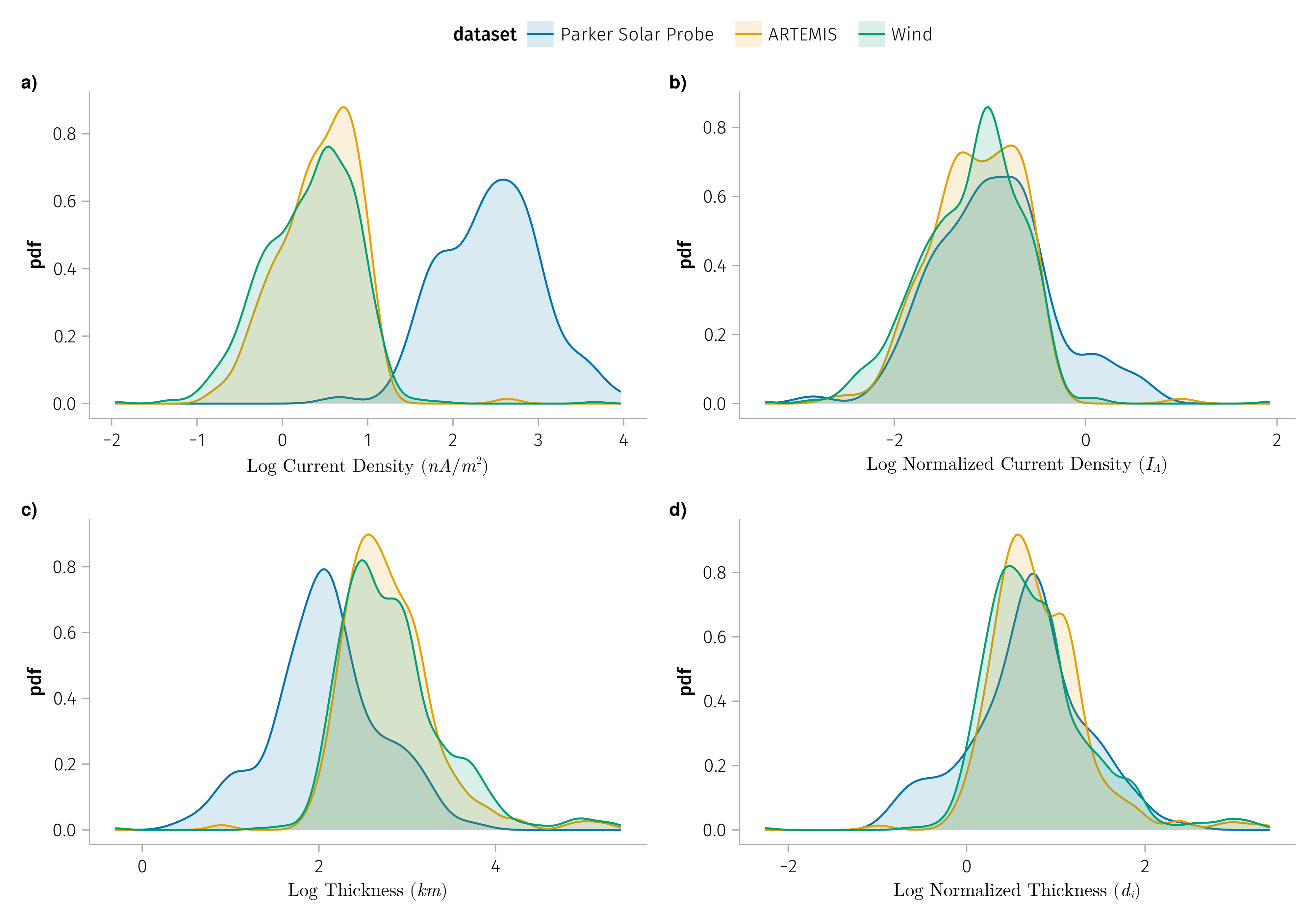
K1: Normalized discontinuities properties does not vary much with radial distance

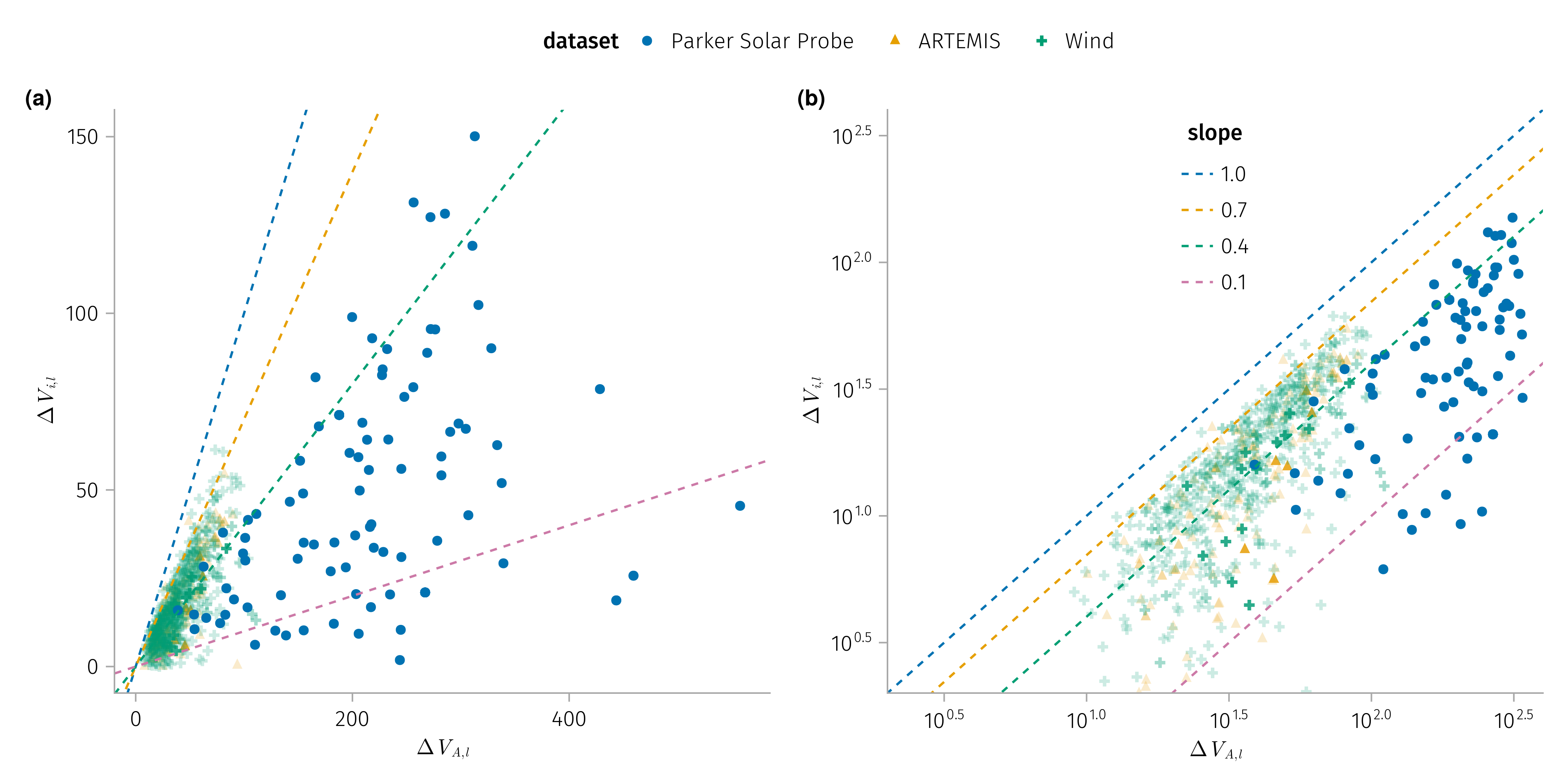
K2: \(Δv_l\),l demonstrates a strong correlation with \(Δv_{A}\), albeit being consistently smaller.

Comparison with Alfven speed and plasma speed change

For rotational discontinuities, the plasma velocity jump across them: the plasma flow velocity \(v_l\) (the solar wind velocity projected onto \(l\)) changes due to changes in \(B_l\), \(Δv_l=±Δv_A\) with \(v_A= B_l / \sqrt{4 n m}\) (Hudson 1970).

Comparison with anisotropy

The equation for \(Δv_A\) includes a factor depending on the anisotropy of the plasma.

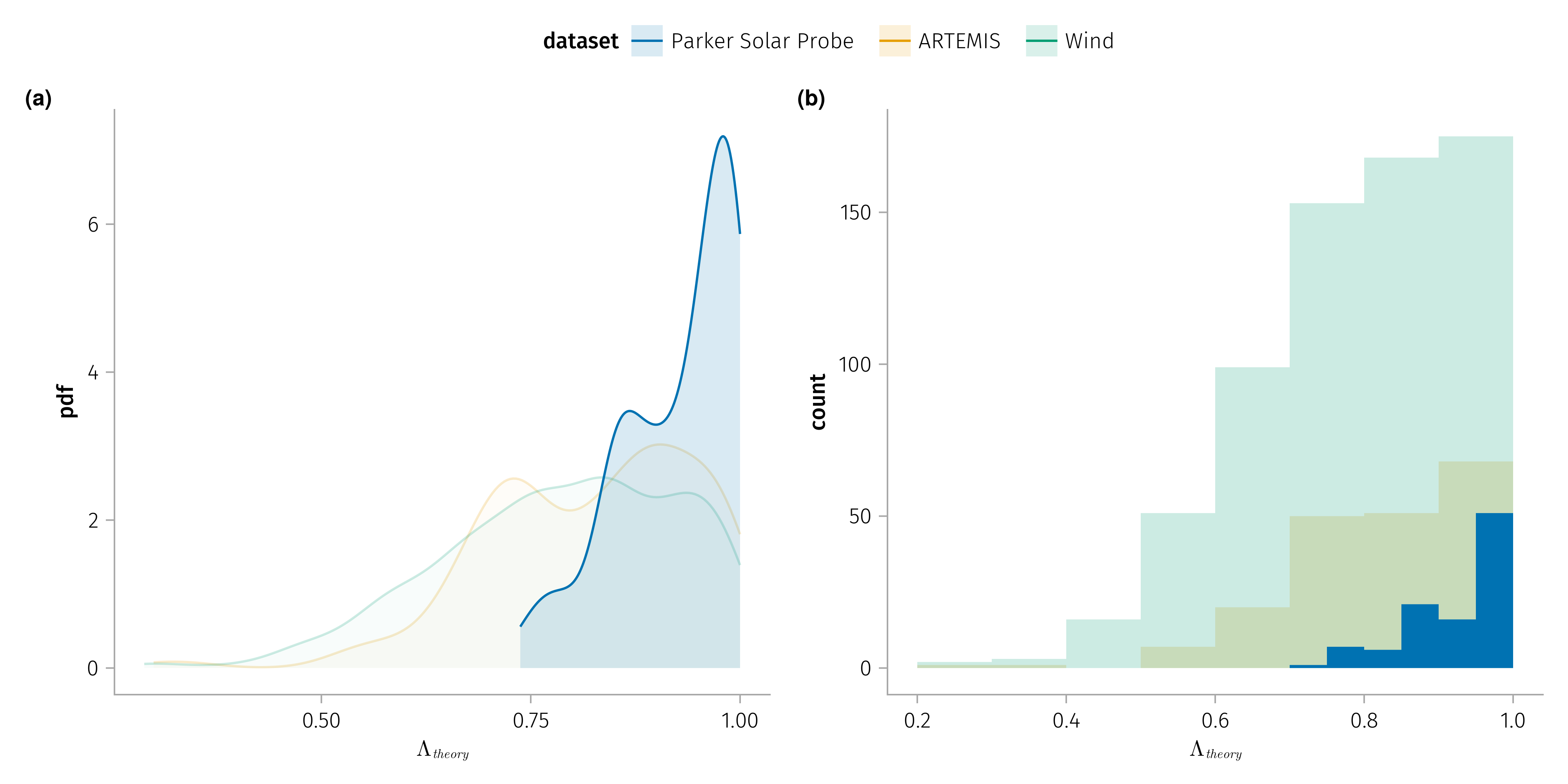
Pressure anisotropy \(Λ = \mu (P_∥ - P_⊥) / B^2\).

Conclusion

  • The properties of the discontinuities is related to the local plasma parameters
    • Thickness => ion inertial length
    • Current density => Alfven velocity (current density)
  • Normalized thickness and current density of discontinuities remain constant with radial distance
  • Anisotropy of the plasma is expected to be larger near the sun to explain the observed speed change ratio \(Δv_i/Δv_A\).

References

Hudson, P. D. 1970. “Discontinuities in an Anisotropic Plasma and Their Identification in the Solar Wind.” Planetary and Space Science 18 (11): 1611–22. https://doi.org/10.1016/0032-0633(70)90036-X.
Liu, Y. Y., H. S. Fu, J. B. Cao, Z. Wang, R. J. He, Z. Z. Guo, Y. Xu, and Y. Yu. 2022. “Magnetic Discontinuities in the Solar Wind and Magnetosheath: Magnetospheric Multiscale Mission (MMS) Observations.” Astrophysical Journal 930 (1): 63. https://doi.org/10.3847/1538-4357/ac62d2.
Perrone, Denise, D Stansby, T S Horbury, and L Matteini. 2019. “Radial Evolution of the Solar Wind in Pure High-Speed Streams: HELIOS Revised Observations.” Monthly Notices of the Royal Astronomical Society 483 (3): 3730–37. https://doi.org/10.1093/mnras/sty3348.