Poor man’s magnetometer

Plot the energy recorded versus the incident energy

Plot the energy recorded (past the Al) versus the incident energy, for beams of various energies, and for different thickness (10nm, 100nm, …). Use H+, He+, O+. Use SPENVIS or GEANT-4 for your modeling.

The energy loss of particles depends on the nature of particles (mass, charge, etc), the incident energy, and the thickness of the Al layer.

For the two-layer detector, where the first layer is Al and the second layer is Silicon, the thickness of the Al layer varies from 0 nm to 100 nm with the thickness of the Si layer fixed to 2 mm.

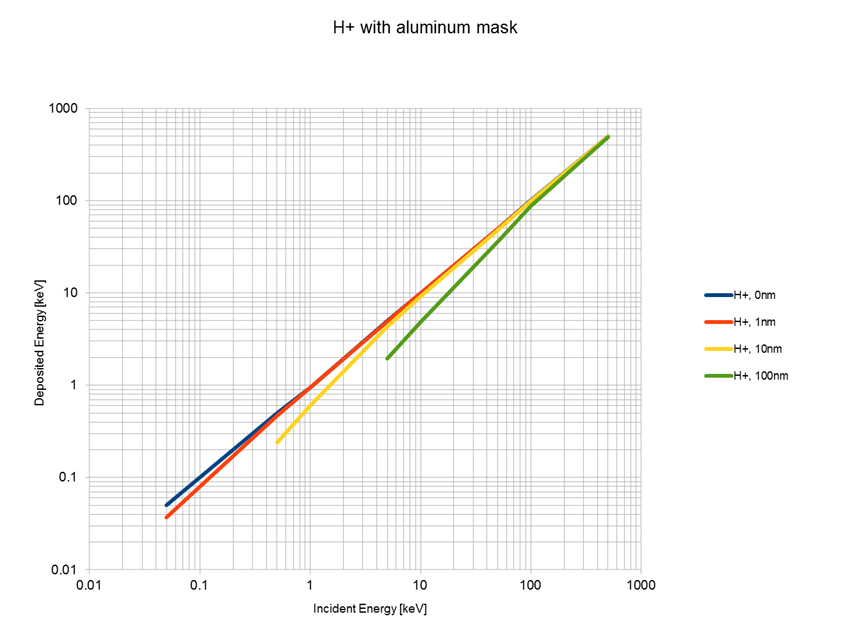
As shown in Figure 1, heavier ions like O+ deposits more energy in the Al layer than lighter ions like He+ and H+, leading to a smaller energy recorded by the Si layer.

And for O+ with low incoming energy below a certain energy threshold \(E\), the recorded deposited energy in Si layer will drop to zero. This threshold energy \(E\) depends on the thickness of the Al layer \(d\). The thicker the Al layer, the higher the threshold energy.

\[E=E(d)\]

More generally, the threshold energy \(E\) also depends the incident particle \(s\).

\[E=E(d,s)\]

Code 
using Pkg
Pkg.add([
    "YAML",
    "DataFrames",
    "Gadfly",
    "Unitful",
])

using YAML
using DataFrames
using Gadfly
using Unitful
Code 
function parse_result_line(line)
    values = split(line, ',')
    Layer = parse(Int, values[1])
    Thickness = parse(Float64, values[2])  # Assuming thickness in cm
    Density = parse(Float64, values[3])    # Assuming density in g/cm3
    Dose = parse(Float64, values[4])       # Assuming dose in keV
    Error = try
        parse(Float64, values[5])
    catch _
        NaN
    end  # Handle '-nan' and other errors

    return (Layer, Thickness, Density, Dose, Error)
end

function convert_data(yaml_data)
    # Iterate through the data and convert each field
    for entry in yaml_data
        entry["layer.Al.thickness"] = parse(Float64, replace(entry["layer.Al.thickness"], " um" => "")) * 1000 * u"nm"
        entry["source"]["energy"] = parse(Float64, replace(entry["source"]["energy"], " MeV" => "")) * 1000
        entry["result"] = [parse_result_line(line) for line in split(entry["result"], '\n') if line != ""]
    end

    df = DataFrame(
        IncidentEnergy=[entry["source"]["energy"] for entry in yaml_data],
        DepositedEnergy=[entry["result"][3][4] for entry in yaml_data],
        SourceParticle=[entry["source"]["particle"] for entry in yaml_data],
        LayerAlThickness=[entry["layer.Al.thickness"] for entry in yaml_data],
    )

    return df
end
convert_data (generic function with 1 method)
Code 
function read_data(filename="result.yml")
    # Read YAML file or string
    filepath = joinpath(@__DIR__, "run", filename)
    # Parse YAML content
    parsed_data = YAML.load_file(filepath)

    # Convert data to DataFrame
    df = convert_data(parsed_data)

    return df
end
read_data (generic function with 2 methods)

The result from SPENVIS is stored in a yaml file. We parse it and convert it to DataFrame for analysis.

Code 
df = read_data()
26×4 DataFrame
Row IncidentEnergy DepositedEnergy SourceParticle LayerAlThickness
Float64 Float64 String Quantity…
1 10.0 9.13347 proton 10.0 nm
2 1000.0 999.495 proton 10.0 nm
3 10.0 4.21557 proton 100.0 nm
4 1000.0 994.992 proton 100.0 nm
5 10.0 9.2096 alpha 10.0 nm
6 1000.0 996.43 alpha 10.0 nm
7 10.0 1.48217 alpha 100.0 nm
8 1000.0 964.217 alpha 100.0 nm
9 5.0 4.15482 alpha 10.0 nm
10 5.0 0.0332675 alpha 100.0 nm
11 10.0 0.0 o+ 100.0 nm
12 1000.0 854.274 o+ 100.0 nm
13 1000.0 984.925 o+ 10.0 nm
14 100.0 95.0629 o+ 10.0 nm
15 50.0 45.8783 o+ 10.0 nm
16 20.0 15.5834 o+ 10.0 nm
17 10.0 2.62646 o+ 10.0 nm
18 8.0 0.678313 o+ 10.0 nm
19 5.0 0.0383982 o+ 10.0 nm
20 5.0 0.757253 proton 100.0 nm
21 100.0 86.8131 proton 100.0 nm
22 100.0 75.4222 alpha 100.0 nm
23 100.0 51.4169 o+ 100.0 nm
24 50.0 2.86204 o+ 100.0 nm
25 40.0 0.0961512 o+ 100.0 nm
26 40.0 25.4273 alpha 100.0 nm
Code 
# Plot data with x = IncidentEnergy, y = DepositedEnergy, color = SourceParticle, facet = LayerAlThickness, using log scale on x-axis and y-axis

plot(df,
    x=:IncidentEnergy,
    y=:DepositedEnergy,
    color=:SourceParticle,
    shape=:SourceParticle,
    xgroup=:LayerAlThickness,
    Geom.subplot_grid(Geom.line, Geom.point),
    Scale.x_log10, Scale.y_log10,
)
# plot(df, x=:IncidentEnergy, y=:DepositedEnergy, color=:SourceParticle, linestyle=:LayerAlThickness, Geom.line, Scale.x_log10, Scale.y_log10)
IncidentEnergy by LayerAlThickness proton alpha o+ SourceParticle 100.0 nm 10.0 nm 100 101 102 103 100.0 100.1 100.2 100.3 100.4 100.5 100.6 100.7 100.8 100.9 101.0 101.1 101.2 101.3 101.4 101.5 101.6 101.7 101.8 101.9 102.0 102.1 102.2 102.3 102.4 102.5 102.6 102.7 102.8 102.9 103.0 100.00 100.01 100.02 100.03 100.04 100.05 100.06 100.07 100.08 100.09 100.10 100.11 100.12 100.13 100.14 100.15 100.16 100.17 100.18 100.19 100.20 100.21 100.22 100.23 100.24 100.25 100.26 100.27 100.28 100.29 100.30 100.31 100.32 100.33 100.34 100.35 100.36 100.37 100.38 100.39 100.40 100.41 100.42 100.43 100.44 100.45 100.46 100.47 100.48 100.49 100.50 100.51 100.52 100.53 100.54 100.55 100.56 100.57 100.58 100.59 100.60 100.61 100.62 100.63 100.64 100.65 100.66 100.67 100.68 100.69 100.70 100.71 100.72 100.73 100.74 100.75 100.76 100.77 100.78 100.79 100.80 100.81 100.82 100.83 100.84 100.85 100.86 100.87 100.88 100.89 100.90 100.91 100.92 100.93 100.94 100.95 100.96 100.97 100.98 100.99 101.00 101.01 101.02 101.03 101.04 101.05 101.06 101.07 101.08 101.09 101.10 101.11 101.12 101.13 101.14 101.15 101.16 101.17 101.18 101.19 101.20 101.21 101.22 101.23 101.24 101.25 101.26 101.27 101.28 101.29 101.30 101.31 101.32 101.33 101.34 101.35 101.36 101.37 101.38 101.39 101.40 101.41 101.42 101.43 101.44 101.45 101.46 101.47 101.48 101.49 101.50 101.51 101.52 101.53 101.54 101.55 101.56 101.57 101.58 101.59 101.60 101.61 101.62 101.63 101.64 101.65 101.66 101.67 101.68 101.69 101.70 101.71 101.72 101.73 101.74 101.75 101.76 101.77 101.78 101.79 101.80 101.81 101.82 101.83 101.84 101.85 101.86 101.87 101.88 101.89 101.90 101.91 101.92 101.93 101.94 101.95 101.96 101.97 101.98 101.99 102.00 102.01 102.02 102.03 102.04 102.05 102.06 102.07 102.08 102.09 102.10 102.11 102.12 102.13 102.14 102.15 102.16 102.17 102.18 102.19 102.20 102.21 102.22 102.23 102.24 102.25 102.26 102.27 102.28 102.29 102.30 102.31 102.32 102.33 102.34 102.35 102.36 102.37 102.38 102.39 102.40 102.41 102.42 102.43 102.44 102.45 102.46 102.47 102.48 102.49 102.50 102.51 102.52 102.53 102.54 102.55 102.56 102.57 102.58 102.59 102.60 102.61 102.62 102.63 102.64 102.65 102.66 102.67 102.68 102.69 102.70 102.71 102.72 102.73 102.74 102.75 102.76 102.77 102.78 102.79 102.80 102.81 102.82 102.83 102.84 102.85 102.86 102.87 102.88 102.89 102.90 102.91 102.92 102.93 102.94 102.95 102.96 102.97 102.98 102.99 103.00 100 103 100 101 102 103 100.0 100.1 100.2 100.3 100.4 100.5 100.6 100.7 100.8 100.9 101.0 101.1 101.2 101.3 101.4 101.5 101.6 101.7 101.8 101.9 102.0 102.1 102.2 102.3 102.4 102.5 102.6 102.7 102.8 102.9 103.0 100.00 100.01 100.02 100.03 100.04 100.05 100.06 100.07 100.08 100.09 100.10 100.11 100.12 100.13 100.14 100.15 100.16 100.17 100.18 100.19 100.20 100.21 100.22 100.23 100.24 100.25 100.26 100.27 100.28 100.29 100.30 100.31 100.32 100.33 100.34 100.35 100.36 100.37 100.38 100.39 100.40 100.41 100.42 100.43 100.44 100.45 100.46 100.47 100.48 100.49 100.50 100.51 100.52 100.53 100.54 100.55 100.56 100.57 100.58 100.59 100.60 100.61 100.62 100.63 100.64 100.65 100.66 100.67 100.68 100.69 100.70 100.71 100.72 100.73 100.74 100.75 100.76 100.77 100.78 100.79 100.80 100.81 100.82 100.83 100.84 100.85 100.86 100.87 100.88 100.89 100.90 100.91 100.92 100.93 100.94 100.95 100.96 100.97 100.98 100.99 101.00 101.01 101.02 101.03 101.04 101.05 101.06 101.07 101.08 101.09 101.10 101.11 101.12 101.13 101.14 101.15 101.16 101.17 101.18 101.19 101.20 101.21 101.22 101.23 101.24 101.25 101.26 101.27 101.28 101.29 101.30 101.31 101.32 101.33 101.34 101.35 101.36 101.37 101.38 101.39 101.40 101.41 101.42 101.43 101.44 101.45 101.46 101.47 101.48 101.49 101.50 101.51 101.52 101.53 101.54 101.55 101.56 101.57 101.58 101.59 101.60 101.61 101.62 101.63 101.64 101.65 101.66 101.67 101.68 101.69 101.70 101.71 101.72 101.73 101.74 101.75 101.76 101.77 101.78 101.79 101.80 101.81 101.82 101.83 101.84 101.85 101.86 101.87 101.88 101.89 101.90 101.91 101.92 101.93 101.94 101.95 101.96 101.97 101.98 101.99 102.00 102.01 102.02 102.03 102.04 102.05 102.06 102.07 102.08 102.09 102.10 102.11 102.12 102.13 102.14 102.15 102.16 102.17 102.18 102.19 102.20 102.21 102.22 102.23 102.24 102.25 102.26 102.27 102.28 102.29 102.30 102.31 102.32 102.33 102.34 102.35 102.36 102.37 102.38 102.39 102.40 102.41 102.42 102.43 102.44 102.45 102.46 102.47 102.48 102.49 102.50 102.51 102.52 102.53 102.54 102.55 102.56 102.57 102.58 102.59 102.60 102.61 102.62 102.63 102.64 102.65 102.66 102.67 102.68 102.69 102.70 102.71 102.72 102.73 102.74 102.75 102.76 102.77 102.78 102.79 102.80 102.81 102.82 102.83 102.84 102.85 102.86 102.87 102.88 102.89 102.90 102.91 102.92 102.93 102.94 102.95 102.96 102.97 102.98 102.99 103.00 100 103 1.60205999132796231.4053007594228677 1.6020599913279623-1.0170453815831295 1.69897000433601870.4566763061569218 2.01.7111056354514849 2.01.8774990810832295 2.01.9385852646746489 0.6989700043360189-0.1207589401012299 3.02.931597137886862 1.0,-Inf 0.6989700043360189-1.4779802260869588 3.02.98417482925214 1.00.17089743261618665 3.02.9978197635088732 1.00.6248567172906062 0.6989700043360189-1.415689472972055 0.9030899869919435-0.16856960341474359 1.00.4193712871079017 1.30102999566398131.1926613823570411 1.69897000433601871.6616075062630538 2.01.978011058799333 3.02.993403028848327 0.69897000433601890.6185523180390649 3.02.9984467945753503 1.00.9642406736070522 3.02.9997807127927865 1.00.9606359017187183 10-2 10-1 100 101 102 103 10-2.0 10-1.8 10-1.6 10-1.4 10-1.2 10-1.0 10-0.8 10-0.6 10-0.4 10-0.2 100.0 100.2 100.4 100.6 100.8 101.0 101.2 101.4 101.6 101.8 102.0 102.2 102.4 102.6 102.8 103.0 10-2.00 10-1.98 10-1.96 10-1.94 10-1.92 10-1.90 10-1.88 10-1.86 10-1.84 10-1.82 10-1.80 10-1.78 10-1.76 10-1.74 10-1.72 10-1.70 10-1.68 10-1.66 10-1.64 10-1.62 10-1.60 10-1.58 10-1.56 10-1.54 10-1.52 10-1.50 10-1.48 10-1.46 10-1.44 10-1.42 10-1.40 10-1.38 10-1.36 10-1.34 10-1.32 10-1.30 10-1.28 10-1.26 10-1.24 10-1.22 10-1.20 10-1.18 10-1.16 10-1.14 10-1.12 10-1.10 10-1.08 10-1.06 10-1.04 10-1.02 10-1.00 10-0.98 10-0.96 10-0.94 10-0.92 10-0.90 10-0.88 10-0.86 10-0.84 10-0.82 10-0.80 10-0.78 10-0.76 10-0.74 10-0.72 10-0.70 10-0.68 10-0.66 10-0.64 10-0.62 10-0.60 10-0.58 10-0.56 10-0.54 10-0.52 10-0.50 10-0.48 10-0.46 10-0.44 10-0.42 10-0.40 10-0.38 10-0.36 10-0.34 10-0.32 10-0.30 10-0.28 10-0.26 10-0.24 10-0.22 10-0.20 10-0.18 10-0.16 10-0.14 10-0.12 10-0.10 10-0.08 10-0.06 10-0.04 10-0.02 100.00 100.02 100.04 100.06 100.08 100.10 100.12 100.14 100.16 100.18 100.20 100.22 100.24 100.26 100.28 100.30 100.32 100.34 100.36 100.38 100.40 100.42 100.44 100.46 100.48 100.50 100.52 100.54 100.56 100.58 100.60 100.62 100.64 100.66 100.68 100.70 100.72 100.74 100.76 100.78 100.80 100.82 100.84 100.86 100.88 100.90 100.92 100.94 100.96 100.98 101.00 101.02 101.04 101.06 101.08 101.10 101.12 101.14 101.16 101.18 101.20 101.22 101.24 101.26 101.28 101.30 101.32 101.34 101.36 101.38 101.40 101.42 101.44 101.46 101.48 101.50 101.52 101.54 101.56 101.58 101.60 101.62 101.64 101.66 101.68 101.70 101.72 101.74 101.76 101.78 101.80 101.82 101.84 101.86 101.88 101.90 101.92 101.94 101.96 101.98 102.00 102.02 102.04 102.06 102.08 102.10 102.12 102.14 102.16 102.18 102.20 102.22 102.24 102.26 102.28 102.30 102.32 102.34 102.36 102.38 102.40 102.42 102.44 102.46 102.48 102.50 102.52 102.54 102.56 102.58 102.60 102.62 102.64 102.66 102.68 102.70 102.72 102.74 102.76 102.78 102.80 102.82 102.84 102.86 102.88 102.90 102.92 102.94 102.96 102.98 103.00 10-3 100 103 DepositedEnergy
Figure 1: Deposited energy as a function of incident energy with different Al layer thickness.

Differentiate monoenergetic ions

Demonstrate that with a sufficient number of detectors you could differentiate monoenergetic protons, He+ and O+.

Assuming the Protons constitute \(n_1\) percen, He+ \(n_2\), and O+ \(n_3\) of the incoming beam. For three unknown variables \(n_1\), \(n_2\), \(n_3\), we need at least three detectors to solve the equation system. With the first detector recording the total incoming energy \(E_1\), the second detector \(E_2\), and the third detector \(E_3\), we have the following equation system:

\[E_1 = n_1 E + n_2 E + n_3 E\] \[E_2 = n_1 \alpha_{2,p} E + n_2 \alpha_{2,He+} E + n_3 \alpha_{2,O+} E\] \[E_3 = n_1 \alpha_{3,p} E + n_2 \alpha_{3,He+} E + n_3 \alpha_{3,O+} E\]

where \(\alpha_{2,p}\), \(\alpha_{2,He+}\), \(\alpha_{2,O+}\), \(\alpha_{3,p}\), \(\alpha_{3,He+}\), \(\alpha_{3,O+}\) are 1- the energy loss ratio of protons, He+ and O+ in the Al layer of the second and third detector respectively.

Since \(\alpha_{i,p}\) can be determined from experiment/simulation, we can solve the above equation to get \(n_1\), \(n_2\), \(n_3\).

If we want to well differentiate monoenergetic protons, He+ and O+ with energy \(E\), we can reverse the relationship \(E=E(d,s)\) to get the thickness of the Al layer \(d\) for each ion. This is possible because theoretically the threshold energy \(E\) is a monotonic increasing function of the thickness of the Al layer \(d\).

\[d=d(E,s)\]

So for a detector with a thickness \(d_{O+}=d(E,O+)\) of the Al layer, we only detect the deposited energy of protons and He+ in the Si layer. And for a detector with a thickness \(d_{He+}=d(E,He+)\) of the Al layer, we only detect the deposited energy of protons in the Si layer.

Then we have additional \(\alpha_{2,O+}=0\) and \(\alpha_{3,O+}=\alpha_{3,He+}=0\) in the equation system, simplifying the equation system to:

\[E_1 = n_1 E + n_2 E + n_3 E\] \[E_2 = n_1 \alpha_{2,p} E + n_2 \alpha_{2,He+} E\] \[E_3 = n_1 \alpha_{3,p} E\]

To demonstrate the differentiation, suppose the energy of the incoming beam is \(E=100\) keV.

From the Figure 2, we can use the following thickness of the Al layer to differentiate the three ions:

  • \(d_{1} = d_{O+} \approx 300 nm\)
  • \(d_{2} = d_{He+} \approx 610 nm\)

And we have \(\alpha_{2,p} \approx 0.59\), \(\alpha_{2,He+} \approx 0.38\) and \(\alpha_{3,p} \approx 0.22\) from the simulation. The equation is solvable.

Code 
df2 = read_data("result_2.yml")
15×4 DataFrame
Row IncidentEnergy DepositedEnergy SourceParticle LayerAlThickness
Float64 Float64 String Quantity…
1 100.0 54.2355 alpha 200.0 nm
2 100.0 36.5835 alpha 300.0 nm
3 100.0 25.0133 alpha 400.0 nm
4 100.0 20.4553 alpha 500.0 nm
5 100.0 17.9386 alpha 600.0 nm
6 100.0 17.4216 alpha 605.0 nm
7 100.0 0.0 alpha 610.0 nm
8 100.0 0.0 alpha 650.0 nm
9 100.0 22.0127 proton 610.0 nm
10 100.0 51.4169 O+ 100.0 nm
11 100.0 23.1507 O+ 150.0 nm
12 100.0 5.50822 O+ 200.0 nm
13 100.0 0.613181 O+ 250.0 nm
14 100.0 0.0124996 O+ 300.0 nm
15 100.0 59.3796 proton 300.0 nm
Code 
# Plot data with x = LayerAlThickness, y = DepositedEnergy, color = SourceParticle

plot(df2,
    x=:LayerAlThickness,
    y=:DepositedEnergy,
    color=:SourceParticle,
    Geom.line, Geom.point,
)
LayerAlThickness 0.0 nm 200.0 nm 400.0 nm 600.0 nm 800.0 nm 0.0 nm 50.0 nm 100.0 nm 150.0 nm 200.0 nm 250.0 nm 300.0 nm 350.0 nm 400.0 nm 450.0 nm 500.0 nm 550.0 nm 600.0 nm 650.0 nm 700.0 nm 750.0 nm 800.0 nm 0.0 nm 5.0 nm 10.0 nm 15.0 nm 20.0 nm 25.0 nm 30.0 nm 35.0 nm 40.0 nm 45.0 nm 50.0 nm 55.0 nm 60.0 nm 65.0 nm 70.0 nm 75.0 nm 80.0 nm 85.0 nm 90.0 nm 95.0 nm 100.0 nm 105.0 nm 110.0 nm 115.0 nm 120.0 nm 125.0 nm 130.0 nm 135.0 nm 140.0 nm 145.0 nm 150.0 nm 155.0 nm 160.0 nm 165.0 nm 170.0 nm 175.0 nm 180.0 nm 185.0 nm 190.0 nm 195.0 nm 200.0 nm 205.0 nm 210.0 nm 215.0 nm 220.0 nm 225.0 nm 230.0 nm 235.0 nm 240.0 nm 245.0 nm 250.0 nm 255.0 nm 260.0 nm 265.0 nm 270.0 nm 275.0 nm 280.0 nm 285.0 nm 290.0 nm 295.0 nm 300.0 nm 305.0 nm 310.0 nm 315.0 nm 320.0 nm 325.0 nm 330.0 nm 335.0 nm 340.0 nm 345.0 nm 350.0 nm 355.0 nm 360.0 nm 365.0 nm 370.0 nm 375.0 nm 380.0 nm 385.0 nm 390.0 nm 395.0 nm 400.0 nm 405.0 nm 410.0 nm 415.0 nm 420.0 nm 425.0 nm 430.0 nm 435.0 nm 440.0 nm 445.0 nm 450.0 nm 455.0 nm 460.0 nm 465.0 nm 470.0 nm 475.0 nm 480.0 nm 485.0 nm 490.0 nm 495.0 nm 500.0 nm 505.0 nm 510.0 nm 515.0 nm 520.0 nm 525.0 nm 530.0 nm 535.0 nm 540.0 nm 545.0 nm 550.0 nm 555.0 nm 560.0 nm 565.0 nm 570.0 nm 575.0 nm 580.0 nm 585.0 nm 590.0 nm 595.0 nm 600.0 nm 605.0 nm 610.0 nm 615.0 nm 620.0 nm 625.0 nm 630.0 nm 635.0 nm 640.0 nm 645.0 nm 650.0 nm 655.0 nm 660.0 nm 665.0 nm 670.0 nm 675.0 nm 680.0 nm 685.0 nm 690.0 nm 695.0 nm 700.0 nm 705.0 nm 710.0 nm 715.0 nm 720.0 nm 725.0 nm 730.0 nm 735.0 nm 740.0 nm 745.0 nm 750.0 nm 755.0 nm 760.0 nm 765.0 nm 770.0 nm 775.0 nm 780.0 nm 785.0 nm 790.0 nm 795.0 nm 800.0 nm 0.0 nm 1000.0 nm alpha proton O+ SourceParticle 300.0 nm59.37965 300.0 nm0.01249959 250.0 nm0.6131813 200.0 nm5.508216 150.0 nm23.15073 100.0 nm51.41687 610.0 nm22.01271 650.0 nm0.0 610.0 nm0.0 605.0 nm17.42164 600.0 nm17.93862 500.0 nm20.45534 400.0 nm25.01331 300.0 nm36.58353 200.0 nm54.2355 h,j,k,l,arrows,drag to pan i,o,+,-,scroll,shift-drag to zoom r,dbl-click to reset c for coordinates ? for help ? 0 10 20 30 40 50 60 0.0 2.5 5.0 7.5 10.0 12.5 15.0 17.5 20.0 22.5 25.0 27.5 30.0 32.5 35.0 37.5 40.0 42.5 45.0 47.5 50.0 52.5 55.0 57.5 60.0 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4 6.6 6.8 7.0 7.2 7.4 7.6 7.8 8.0 8.2 8.4 8.6 8.8 9.0 9.2 9.4 9.6 9.8 10.0 10.2 10.4 10.6 10.8 11.0 11.2 11.4 11.6 11.8 12.0 12.2 12.4 12.6 12.8 13.0 13.2 13.4 13.6 13.8 14.0 14.2 14.4 14.6 14.8 15.0 15.2 15.4 15.6 15.8 16.0 16.2 16.4 16.6 16.8 17.0 17.2 17.4 17.6 17.8 18.0 18.2 18.4 18.6 18.8 19.0 19.2 19.4 19.6 19.8 20.0 20.2 20.4 20.6 20.8 21.0 21.2 21.4 21.6 21.8 22.0 22.2 22.4 22.6 22.8 23.0 23.2 23.4 23.6 23.8 24.0 24.2 24.4 24.6 24.8 25.0 25.2 25.4 25.6 25.8 26.0 26.2 26.4 26.6 26.8 27.0 27.2 27.4 27.6 27.8 28.0 28.2 28.4 28.6 28.8 29.0 29.2 29.4 29.6 29.8 30.0 30.2 30.4 30.6 30.8 31.0 31.2 31.4 31.6 31.8 32.0 32.2 32.4 32.6 32.8 33.0 33.2 33.4 33.6 33.8 34.0 34.2 34.4 34.6 34.8 35.0 35.2 35.4 35.6 35.8 36.0 36.2 36.4 36.6 36.8 37.0 37.2 37.4 37.6 37.8 38.0 38.2 38.4 38.6 38.8 39.0 39.2 39.4 39.6 39.8 40.0 40.2 40.4 40.6 40.8 41.0 41.2 41.4 41.6 41.8 42.0 42.2 42.4 42.6 42.8 43.0 43.2 43.4 43.6 43.8 44.0 44.2 44.4 44.6 44.8 45.0 45.2 45.4 45.6 45.8 46.0 46.2 46.4 46.6 46.8 47.0 47.2 47.4 47.6 47.8 48.0 48.2 48.4 48.6 48.8 49.0 49.2 49.4 49.6 49.8 50.0 50.2 50.4 50.6 50.8 51.0 51.2 51.4 51.6 51.8 52.0 52.2 52.4 52.6 52.8 53.0 53.2 53.4 53.6 53.8 54.0 54.2 54.4 54.6 54.8 55.0 55.2 55.4 55.6 55.8 56.0 56.2 56.4 56.6 56.8 57.0 57.2 57.4 57.6 57.8 58.0 58.2 58.4 58.6 58.8 59.0 59.2 59.4 59.6 59.8 60.0 0 100 DepositedEnergy
Figure 2: Deposited energy as a function of incident energy with different Al layer thickness.

Others

Directions

  • Geometry Definition
  • Source particles
    • He+
      • Atomic number: 2
      • Nucleon number: 4
  • Material Definition

This will be done by creating a plot of energy deposited in Si as function of input energy. You will use freeware Geant-4 which simulates particle interaction with matter, through a portal: SPENVIS. Various models exist there (very useful site!).

First you have to register, then create a project, then input your model input and output parameters, then make a run and get results one-energy-at-a-time. Once you know how to do that, then you must create an array of inputs and outputs outside of SPENVIS in your favorite plotting package (e.g., excel, python or other). You will then record those results and plot them, one array for protons, another for He+ and another for O+. You can try other species as well, for example O2+ which may be present in the low altitude ionosphere.

  • Assume monoenergetic beams. The program allows you to use a simple ion spectrum. (For the bonus question you have to make a guess on the instrument response function, model it in a simple analytical form, then prove it can be done using Geant-4. You do not have to do the bonus.)

For your report, you should not repeat the steps I mention below, but just execute your outline above and go right to the findings, plots and discussion. In the discussion explain how you use the model to design a detector system (how many detectors, thicknesses, orientations etc) that does the job.

  1. On SPENVIS after registration, name your project and proceed to use Geant-4 “MULASSIS”. You can save your run, and come back to it later.

  2. Your system will be a 3 layer system, where the first layer is air, the second Al of variable thickness and the third Silicon of a mm or two... enough to stop the highest energy of interest. You shoot some particles (10,000 is a good number), and record how much energy is deposited in Si. Excluding losses in the Si (phonons) the lost energy is mainly due to losses in the Aluminum. Pick the source parameters: How many/which ions, charge angle (-22 deg -> 22 deg).

  3. For Geometry you pick the layers above, and for Al choose 0, 1, 10 100 nm, one thickness at a time.

  4. Specify the input as monoenergetic beam.

  5. Specify analysis parameters as mean energy (the mean energy deposited based on the 10,000 particle run)

  6. Create a macro (a bunch of commands that tell Geant-4 what to do) and Run.

  7. See the plot

  8. Output results (2 numbers) into your program next to input energy to build the in/out energy curve.

  9. Repeat, one point at a time.

  10. Plot results for one species and then (in different color) for other species.

  11. Repeat for different Al thicknesses.