Ion scattering by solar wind discontinuities
Introduction
The transport of energetic particles within the heliosphere is significantly influenced by the turbulent magnetic field present in the solar wind. However, this turbulence should not be regarded merely as a collection of random magnetic field fluctuations. Instead, the nonlinear energy cascade process results in the formation of coherent structures. These coherent structures have been shown to act as efficient particle scatterers in non-collisional plasmas (Artemyev et al. 2020).
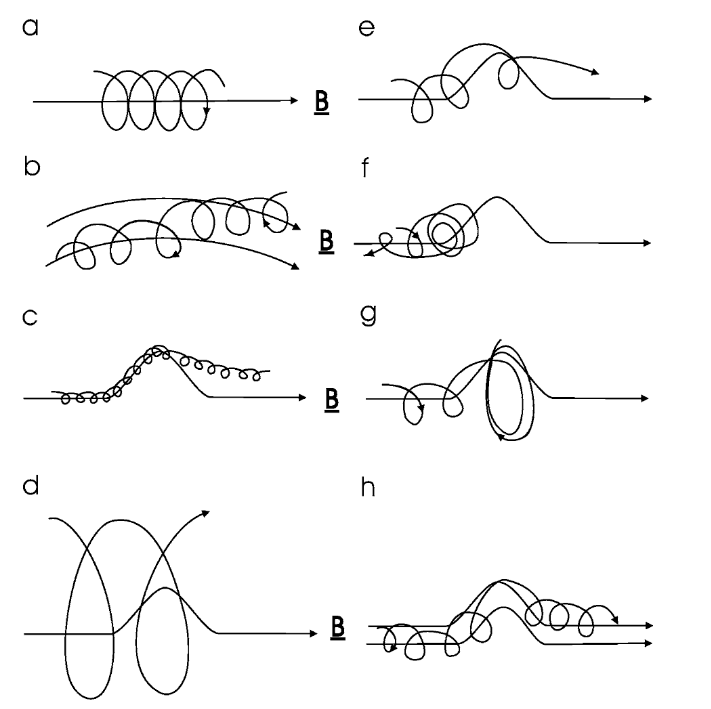
Test particle simulations
\[ \mathbf{B} = B_0 (\cos θ \ e_z + \sin θ ( \sin φ(z) \ e_z + \cos φ (z) \ e_y)) \]
with \(φ(z) = β \tanh(z)\)
Dimensionless form of the motion equation:
\[ \frac{d (γ \mathbf{v})}{dt} = \mathbf{v} \times \mathbf{B} , \frac{d\mathbf{r}}{dt} = \mathbf{v} \]
- \(\mathbf{B} \rightarrow \mathbf{B} / B_0\) : background magnetic field magnitude
- \(\mathbf{r} \rightarrow \mathbf{r} / L\) : discontinuity \(L\)
- \(t \rightarrow t/Ω_0\) : gyroperiod
- \(v \rightarrow v/v_0\) : characteristic velocity \(v_0 = Ω_0 L\)
Parameters
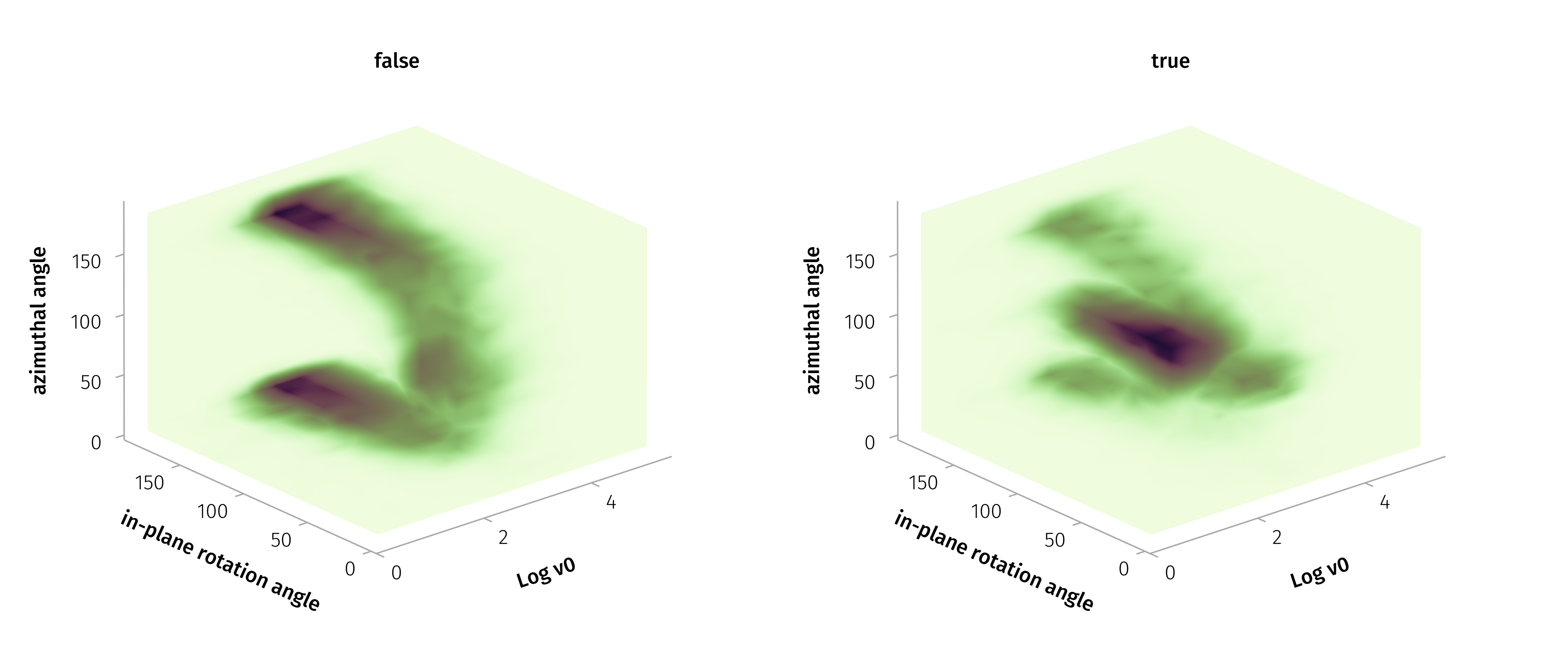
\(Δ|B|/|B| > 0.05\) or \(ω > 60°\)
The most probable values in the 3D distribution are a characteristic velocity (\(v_0\)) of approximately 250 km/s, a in-plane rotation angle (\(ω_{in}\)) about 90 degrees, and an azimuthal angle (\(θ\)) of around 85 degrees.
Examples of Pitch angle scattering
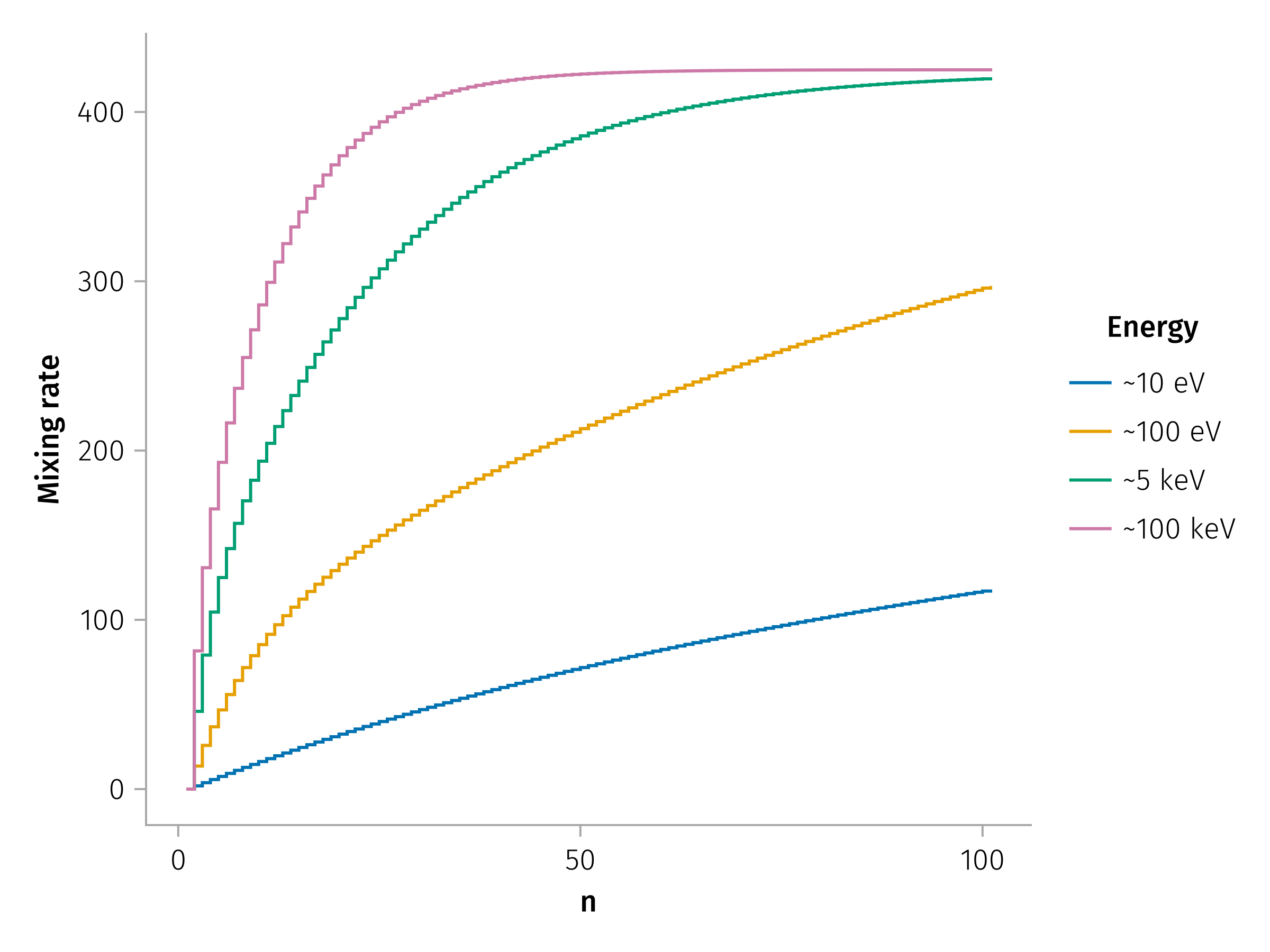
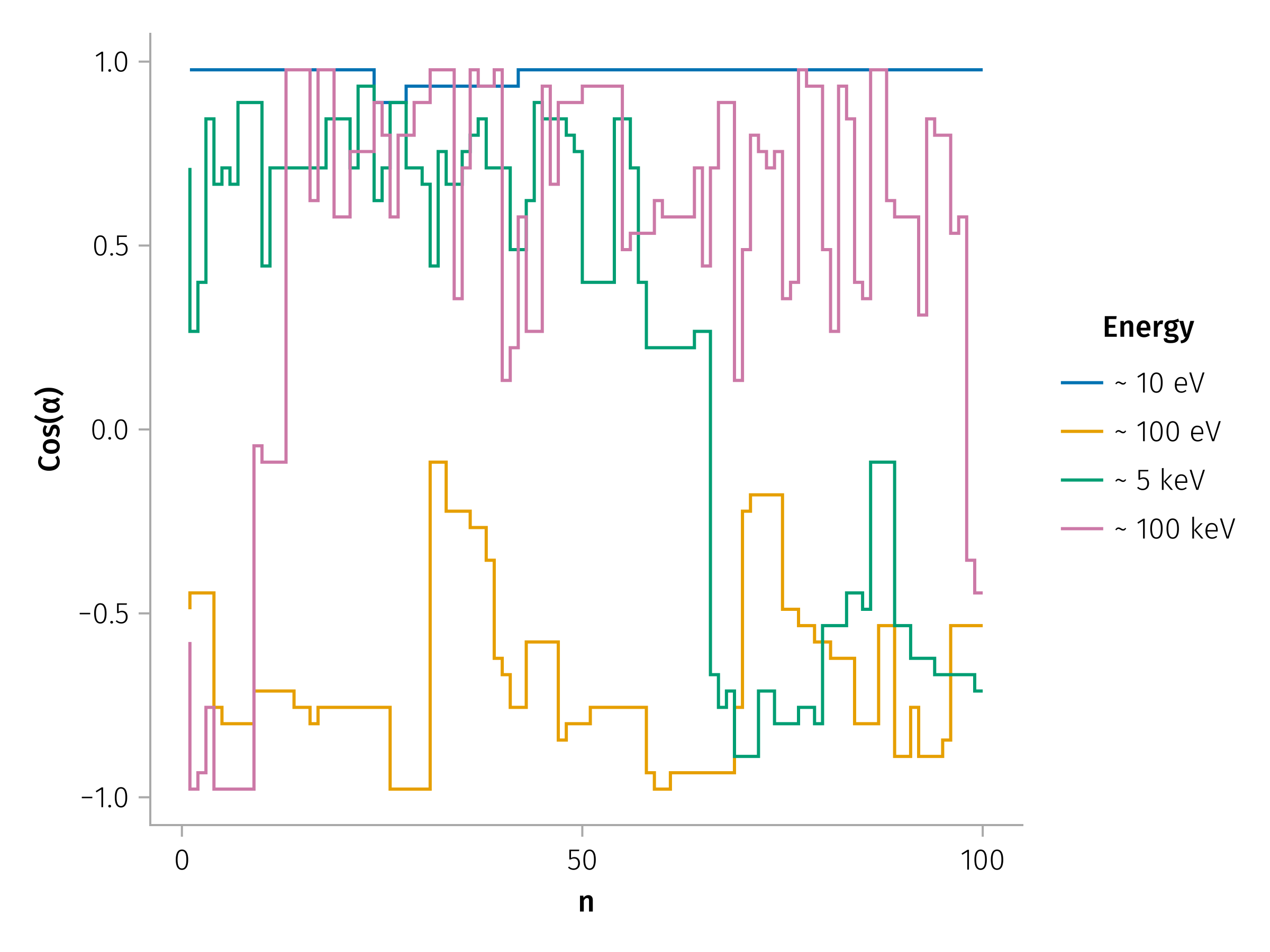
Example of multiple pitch angle scattering for different energies
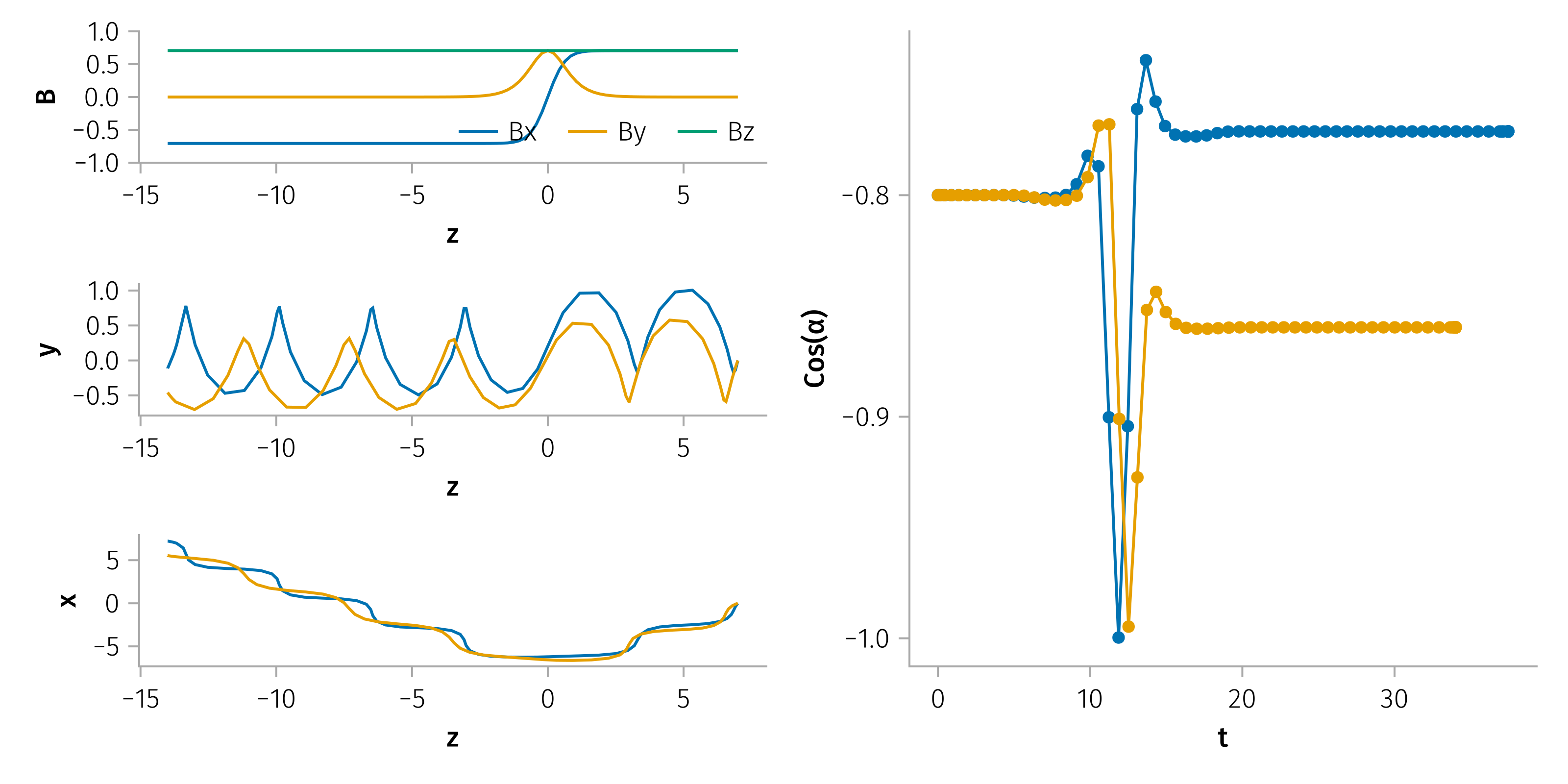
Pitch angle scattering by typical discontinuity
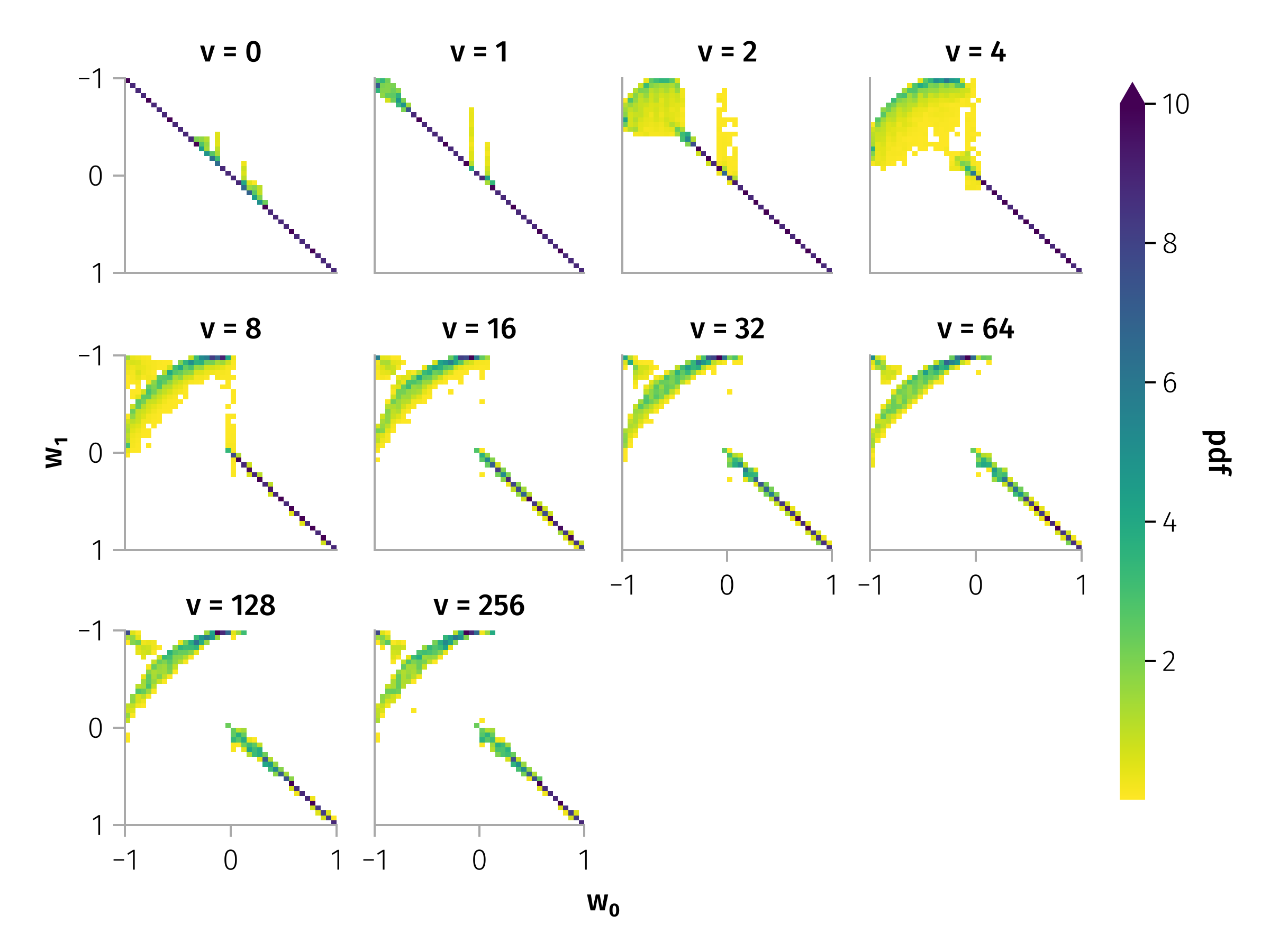
With in-plane rotation angle (\(ω_{in}\)) about 90 degrees, and azimuthal angle (\(θ\)) of around 85 degrees.
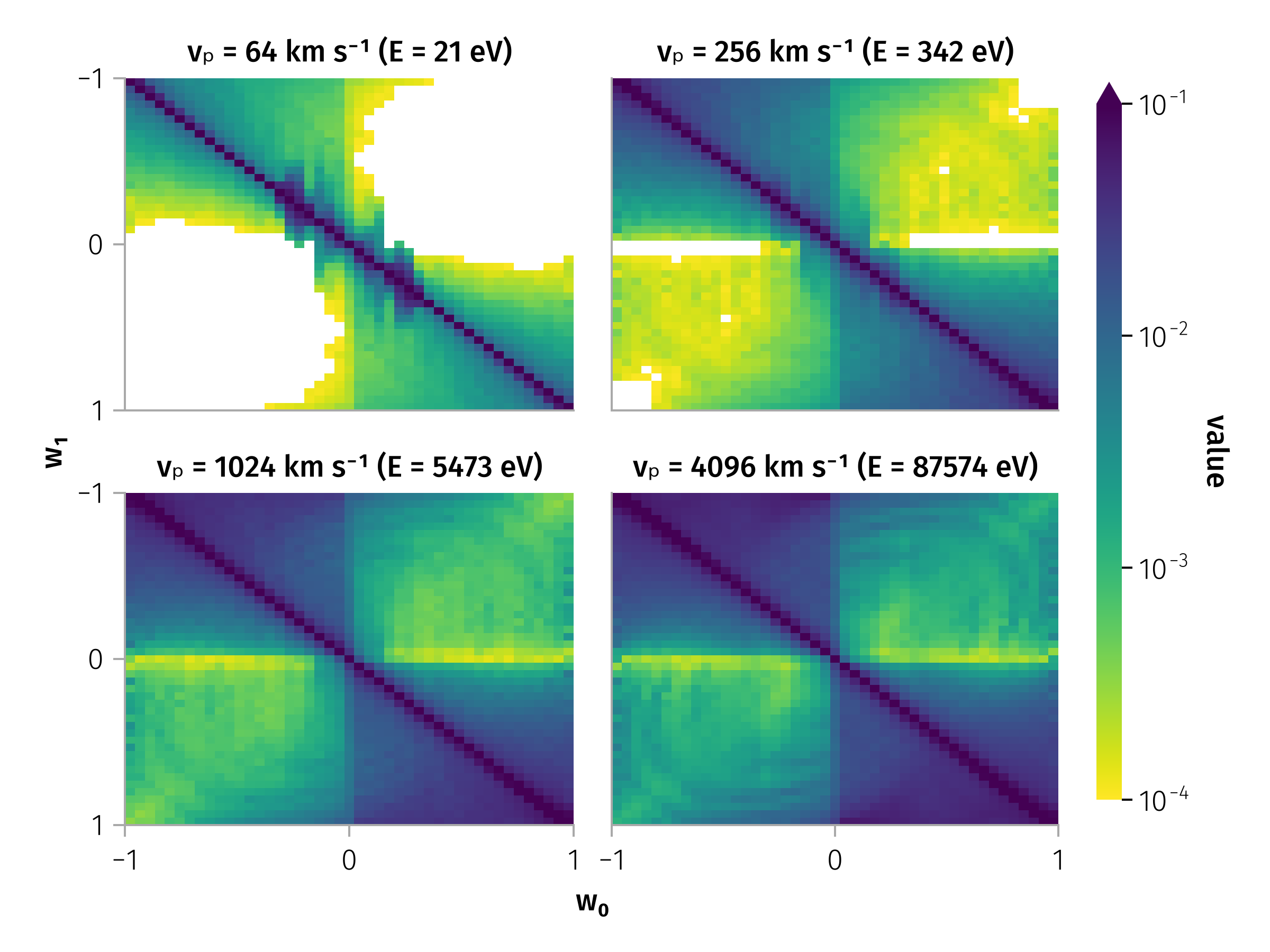
Examples of transition matrix
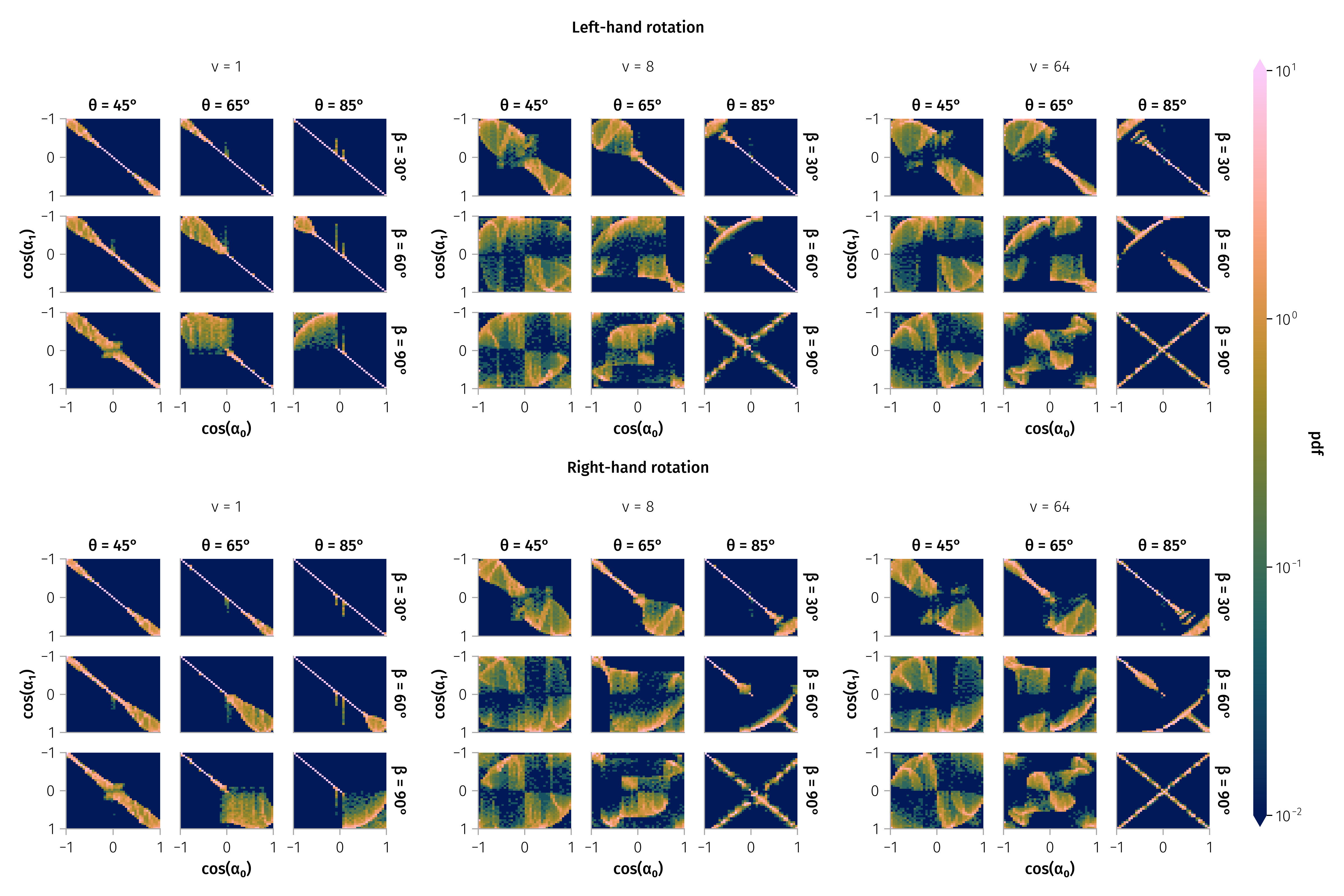
Transition matrix
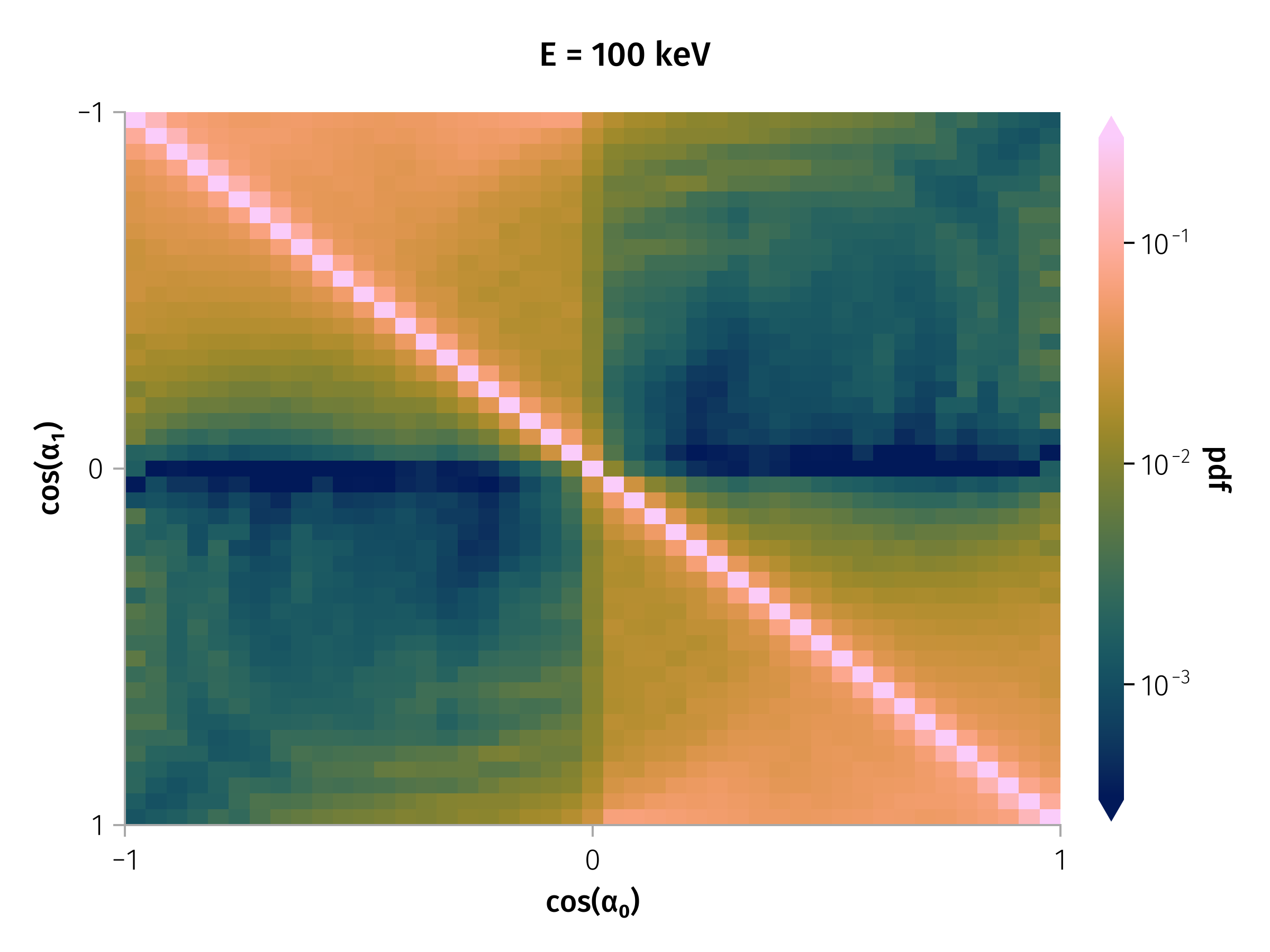
Transition matrix for different particle energies