Thesis Prospectus
Motivation and Significance (Summary)
Solar energetic particles (SEPs), originating from solar flares and coronal mass ejections, pose significant risks to satellite operations, human spaceflight, and communication systems. Accurate prediction of SEP events and their propagation through the heliosphere requires a detailed understanding of particle transport mechanisms in turbulent solar wind environments.
Traditionally, theoretical studies and numerical models of particle transport in the solar wind have focused on turbulence characterized by broadband, low-amplitude, random-phase magnetic fluctuations described by power-law spectra (Jokipii 1966, 1967). However, observations consistently reveal the abundance of intermittent, meso-scale, coherent structures within this turbulent medium, notably current sheets—thin plasma boundaries marked by abrupt magnetic field changes. These current sheets deviate significantly from classical magnetohydrodynamic (MHD) picture due to their kinetic-scale features and strong local magnetic gradients.
Recent theoretical and numerical studies suggest that these coherent structures play a critical role in particle scattering, potentially surpassing the scattering efficiencies predicted by traditional quasilinear theories (Malara, Perri, and Zimbardo 2021; Artemyev et al. 2020). Current sheets, generated naturally through nonlinear turbulence cascades, provide localized regions of intense electromagnetic interactions, leading to enhanced scattering and modification of the particle’s spatial distribution. Despite their demonstrated importance, a quantitative and systematic understanding of how these structures influence SEP transport remains incomplete.
Addressing this critical gap, this dissertation aims to rigorously investigate and quantify the impact of solar wind current sheets on SEP transport processes. Specifically, this research seeks to:
- Characterize the properties and occurrence of current sheets throughout different regions of the heliosphere.
- Develop and validate theoretical models that describe particle scattering induced by these coherent structures.
- Provide a more comprehensive understanding of SEP dynamics, thereby improving predictive capabilities and contributing significantly to space weather modeling.
The motivation for this research lies in the critical need for improved SEP transport models that accurately reflect real-world solar wind conditions. By integrating observational data and advanced theoretical frameworks, this dissertation will provide novel insights into heliospheric particle dynamics, ultimately enhancing our ability to predict and mitigate the risks associated with SEP events.
Research Context and Background
Solar Energetic Particles
(Klein and Dalla 2017; Desai and Giacalone 2016)
Solar energetic particles (SEPs) are high-energy ions and electrons originating at or near the Sun. They span a broad energy spectrum, from Solar energetic particles (SEPs) consist of high-energy ions and electrons originating at or near the Sun. Unlike the solar wind and galactic cosmic rays (GCRs), solar energetic particles (SEPs) manifest as discrete episodic events with intensities that can vary dramatically—by several orders of magnitude—in just minutes. Additionally, SEP events exhibit significant variations in heavy ion composition, spectral shape, and spatial distribution.
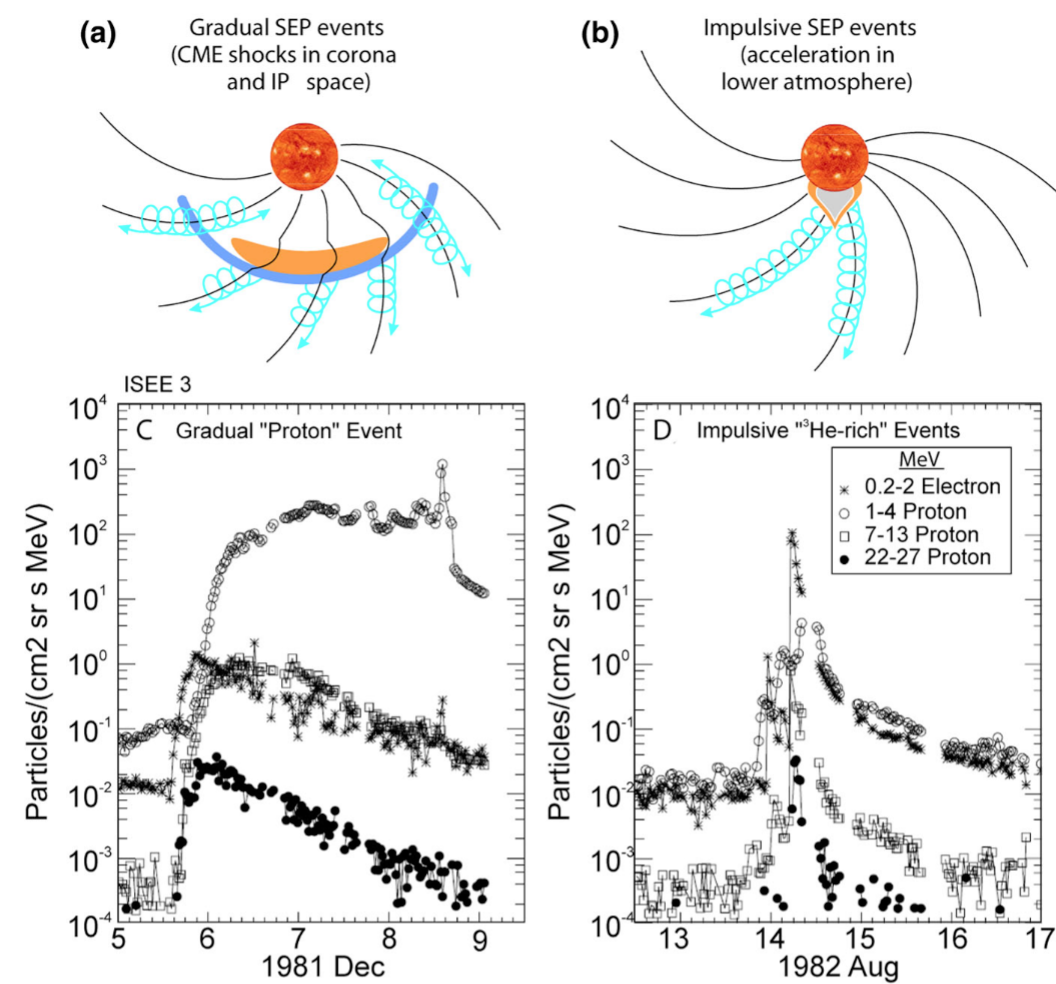
SEPs are primarily accelerated through two distinct mechanisms: (1) magnetic reconnection-driven processes during solar flares, producing impulsive SEP events, and (2) shock-wave acceleration associated with fast coronal mass ejections (CMEs), resulting in large gradual SEP events.
Impulsive SEP events typically have short durations, lasting from minutes to a few hours, and feature characteristically high electron-to-proton ratios and enrichments of heavy ions. In contrast, gradual SEP events are longer-lasting (several days) and are predominantly proton-rich, often associated with fast CMEs driving shocks in the solar corona and interplanetary space. These shocks accelerate particles over extended regions, producing widespread and intense radiation storms.
Turbulent Magnetic Fluctuations
Solar wind turbulence spans scales from the large‑scale coherence length (∼0.01 AU) down to kinetic dissipation scales on the order of the thermal ion gyro‑radius (∼100 km). Of particular importance for energetic particle transport is the turbulence at intermediate scales, often referred to as inertial-range turbulence whose corresponding energy range is about \(1\) GeV to \(1\) keV assuming a \(5\) nT magnetic field. This covers nearly all SEPs as the gyro-radii of almost all SEPs are smaller than the coherence scale and larger than the dissipation scale.
The transport of SEPs through the heliosphere is fundamentally shaped by the properties of magnetic turbulence. Key parameters—such as the spatial inhomogeneity, turbulence level (\(δB/B₀\)), spectral index, and anisotropy of wave vectors (Pucci et al. 2016) —strongly influence how particles scatter in velocity space. These properties govern both parallel and perpendicular transport through mechanisms including pitch-angle diffusion, magnetic field-line meandering, and gradient or curvature drift.
Classical scattering theories and numerical models of particle transport (Giacalone and Jokipii 1999) typically model turbulence as a sea of random, phase-uncorrelated fluctuations (common constructions of magnetic fluctuations for the slab component \(δ𝐁^s\) and two-dimensional component \(δ𝐁^{2D}\) are shown below in Equation 1). However, this idealized view neglects the intricate internal nonlinear structures of turbulence. Increasingly, observations and simulations show that solar wind turbulence is highly intermittent and populated with coherent structures—especially current sheets—that arise naturally through nonlinear cascade processes. These localized structures, often characterized by sharp magnetic field gradients, can trigger rapid and large pitch-angle deflections in energetic particles, significantly enhancing scattering beyond quasilinear predictions.
\[ \begin{aligned} & δ𝐁^s=\sum_{n=1}^{N_m} A_n\left[\cos \alpha_n\left(\cos \phi_n \hat{x}+\sin \phi_n \hat{y}\right)+i \sin \alpha_n(-\right.\left.\left.\sin \phi_n \hat{x}+\cos \phi_n \hat{y}\right)\right] \\ & \times \exp \left(i k_n z+i \beta_n\right) \\ & δ𝐁^{2 D}=\sum_{n=1}^{N_m} A_n i\left(-\sin \phi_n \hat{x}+\cos \phi_n \hat{y}\right) \\ & \times \exp \left[i k_n\left(\cos \phi_n x+\sin \phi_n y\right)+i \beta_n\right] \end{aligned} \tag{1}\]
Therefore, understanding SEP transport requires more than bulk statistical descriptions of turbulence; it demands detailed knowledge of its intermittent nature and the embedded coherent structures that mediate particle scattering. Accurately characterizing these features is essential for developing realistic models of SEP propagation throughout the heliosphere.
Charged Particle Transport and Turbulence Transport Models
The large-scale behavior of energetic charged particles in the heliosphere is commonly described using a diffusive approximation, justified when the particle scattering time is short compared to the timescale of interest. Under this assumption, the evolution of an approximately isotropic particle distribution is governed by the Parker transport equation (Parker 1965). This foundational framework accounts for four main transport processes: spatial diffusion due to particle scattering, advection with the solar wind, drifts (such as gradient and curvature drifts due to variations in the large-scale magnetic field), and adiabatic acceleration:
\[ \frac{∂ f}{∂ t}=\frac{∂}{∂ x_i}\left[\kappa_{i j} \frac{∂ f}{∂ x_j}\right]-U_i \frac{∂ f}{∂ x_i}-V_{d, i} \frac{∂ f}{∂ x_i}+\frac{1}{3} \frac{∂ U_i}{∂ x_i}\left[\frac{∂ f}{∂ \ln p}\right]+ \text{Sources} - \text{Losses}, \tag{2}\]
where \(f\) is the phase-space distribution as a function of the particle momentum, \(p\), position, \(x_i\), and time, \(t\); \(\kappa_{i j}\) is the symmetric part of the diffusion coefficient tensor; \(U_i\) is the bulk plasma velocity; \(V_{d, i}\) is the drift velocity. We note that the drift velocity can be formally derived using guiding center approximation and included in the diffusion tensor as an anti-symmetric part.
The symmetric part of the spatial diffusion tensor can be related to the diffusion coefficient parallel and perpendicular to the magnetic field through \(κ_{ij}=κ_{\perp} \delta_{ij}-\frac{\left(κ_{\perp}-κ_{\|}\right) B_i B_j}{B^2}\). And the spatial transport coefficient along the mean magnetic field can be related to the pitch-angle diffusion coefficient \(D_{\mu\mu}\) (Jokipii, 1966) while the diffusion of energetic particles transverse to the mean magnetic field is less understood.
To better capture the anisotropic nature of particle motion, particularly at early times or near boundaries, the focused transport equation (Roelof, 1969; Skilling, 1971) extends this framework by retaining pitch-angle dependence. This enables a more accurate description of the transition from ballistic to diffusive regimes, especially in regions of strong magnetic field gradients or turbulence. The parallel diffusion coefficient is typically related to the pitch-angle diffusion rate D{}, while the perpendicular diffusion coefficient is influenced by magnetic field line random walk, field inhomogeneity, and drift effects (Jokipii, 1966; Giacalone & Jokipii, 1999). Although is often assumed to be a small fraction of _, recent studies and simulations reveal that perpendicular transport can be significant and energy-dependent.
Moreover, deviations from classical diffusion—such as superdiffusive or subdiffusive behavior—have been observed in SEP events and near interplanetary shocks, challenging the standard Gaussian diffusion paradigm. These non-diffusive transport regimes reflect the complex structure of heliospheric turbulence and often require generalized models based on fractional kinetics or Lévy statistics (Zimbardo et al., 2012; Perri & Zimbardo, 2012; Tautz & Shalchi, 2010). Consequently, the development of accurate turbulence-informed transport models remains central to predicting SEP propagation, especially when accounting for coherent structures and intermittent fluctuations in the solar wind.
Current Sheets in the Solar Wind
Current sheets are characterized by sharp gradients in the magnetic field and plasma properties. Observational studies from spacecraft missions such as Wind, ARTEMIS, and Parker Solar Probe (PSP) consistently detect these structures throughout the heliosphere, from near-Sun regions (~0.1 AU) to the outer heliosphere (~5 AU).
These sheets often exhibit non-ideal behaviors, with kinetic processes such as magnetic reconnection and wave-particle interactions playing essential roles. Understanding the kinetic-scale dynamics within current sheets is therefore vital to fully characterize their impact on particle transport.
Objectives and Thesis Plan
The overall goal of this thesis is to quantify and model the impact of solar wind current sheets on energetic particle transport. This research is structured around two primary objectives:
Observational characterization of solar wind current sheets across the heliosphere
Development and validation of theoretical models for current sheet-induced particle scattering
Work Completed
Observational Analysis of Current Sheets
I have conducted extensive observational analyses using data from spacecraft missions including Juno, Wind, ARTEMIS, and Parker Solar Probe. Key findings include:
Statistical characterization of current sheet occurrence rates, thicknesses, current densities, and magnetic field rotations at multiple radial distances (0.1–5 AU).
Demonstration of persistent and efficient particle scattering by current sheets throughout the inner heliosphere.
Identification of radial scaling laws governing current sheet properties, revealing consistent kinetic-scale behaviors despite changes in heliospheric conditions.
Quantitative Modeling of Particle Scattering
Leveraging the observational data, I developed a theoretical and numerical framework to quantify the efficiency of pitch-angle scattering induced by current sheets. Achievements in this area include:
Formulation of an analytical Hamiltonian model coupled with numerical simulations to evaluate pitch-angle diffusion rates.
Validation of this model using spacecraft observations, confirming significant scattering rates for 100 keV–1 MeV protons.
Demonstration that scattering processes driven by current sheets substantially exceed predictions from classical quasilinear theories, thus revising our understanding of particle transport dynamics.
Multifuid Model for Current Sheet Alfvénicity
To address discrepancies observed in the classical single-fluid MHD description of current sheets, I developed a multifluid model that accounts for kinetic properties of plasma populations. This model:
Explains observed variations in Alfvénicity (the ratio of plasma velocity jump to Alfvén velocity jump) in solar wind current sheets.
Illustrates the transition from single-fluid dominance near the Sun to a multifluid regime at 1 AU, better matching observational data.
Proposed Research Direction
Spatial Diffusion Model Refinement
Building on previous results, the next phase of research will extend the pitch-angle scattering framework to comprehensively model spatial diffusion processes (both parallel and perpendicular). This extension is crucial for accurately capturing the full scope of SEP transport influenced by current sheets.
Methodology
The following methodological steps will guide the refinement of the diffusion model:
Data Integration: Incorporate comprehensive multi-spacecraft datasets spanning radial distances from 0.1 to 5 AU to calibrate and validate the spatial diffusion model.
Numerical Simulation: Utilize advanced particle-in-cell (PIC) and test-particle simulations to systematically quantify spatial diffusion coefficients under realistic solar wind conditions.
Analytical Development: Extend existing analytical frameworks to predict spatial diffusion behaviors informed by numerical simulation results.
Timeline
Months 1–4:
Refine the pitch-angle scattering model to include parallel and perpendicular spatial diffusion.
Perform detailed numerical simulations incorporating observational data from multiple spacecraft.
Months 5–7:
Validate the refined spatial diffusion model using observational data.
Conduct comprehensive statistical analyses to quantify diffusion coefficients at various radial distances.
Months 8–10:
Finalize model development, analyze implications for SEP transport, and prepare dissertation chapters.
Integrate observational and theoretical findings into comprehensive thesis documentation.
Relevance and Broader Implications
This thesis substantially advances our understanding of particle transport mechanisms within turbulent space plasmas, offering significant enhancements to SEP prediction models. By accurately quantifying the influence of coherent structures such as current sheets, the research outcomes have direct applications to improving space weather forecasting, enhancing spacecraft operational safety, and contributing to the broader understanding of plasma turbulence.
Opportunities for Future Research
Completion of this thesis opens several avenues for future investigations:
Exploration of current sheet interactions in other astrophysical environments, such as supernova remnants and planetary magnetospheres.
Advanced integration of machine learning techniques with numerical simulations to further refine SEP transport models.
Expanded observational campaigns utilizing upcoming spacecraft missions designed to probe heliospheric turbulence and particle dynamics at unprecedented resolution.